More Model ω-Questions
Posted by Urs Schreiber
Here are some further questions related to model category theory in general and the folk model structure on -categories in particular, concerned with
- fibrant objects in -categories;
- model structure on -groupoids and crossed complexes;
- general question about weak universal property of homotopy (co)limits.
Fibrant objects and -groupoids
It seems that generically in model categories of “higher structures” the fibrant objects are close to being -groupoids.
This is true for at least one model structure on simplicial sets: fibrant objects here are precisely the Kan complexes. It seems to be also true in and , though I need to check that reference again.
So I am wondering whether the fibrant objects in -categories are related to the -groupoids (well, either those with strict or with weak inverses, I am not sure yet). Is anything known in general?
Model structure on crossed complexes
I have only just started looking at
R. Brown, M. Golasinski, A model structure for the homotopy theory of crossed complexes which describes parts of a model category structure on the category of crossed complexes.
Now, of course by R. Brown and P. Higgins On the algebra of cubes it is well known that crossed complexes are precisely equivalent to -groupoids, i.e. to those -categories for which each cell has a strict inverse cell.
So the obvious question is: How is the Brown-Higgins model structure on crossed complexes related to the folk model structure on -categories? One would hope that the former is precisely the restriction of the latter to -groupoids. Is anything known about this?
Homotopy colimits
I was reading about homotopy (co)limits in Chachólski-Scherer’s very nice Homtopy theory of diagrams especially around page 15 which reviews the special simple case of ordinary push-outs.
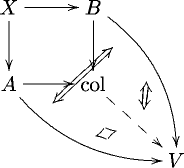
I am wondering: suppose the case mentioned in the middle of this page, that the homotopy colimit happens to be weakly equivalent to the ordinary colimit. Then intuitively the following ought to be right:
given any pushout cone which commutes only up to left or right homotopy in the model category sense, does the expected universal arrow exist anyway, up to left/right homotopy, making the expected diagrams commute, up to left/right homotopy?
This must be an elementary thing, I’d be grateful for a pointer to the literature.

Re: More Model ω-Questions
Concerning the thirdd question, on the relation between homotopy colimits and weak/lax colimits I am being pointed to the classical result by Thomason
R. Thomason, Homotopy colimits in the category of all small categories
reviewed for instance in
Murray Heggie, Homotopy colimits in presheaf categories appearing on p. 5 there,
which says that the Grothendieck construction on a weak/lax functor , which is the weak/lax colimit of that functor, is equivalent to the homotopy colimit of that functor
using a model structure which in Thomason’s original article was induced from one on simplicial sets (after passing to nerves), and which has meanwhile be turned into a model structure on Cat called the Thomason model structure.
This has recently been generalized to -fold categories (strict cubical -categories) in
Fiore, Paoli, A Thomason Model Structure on the Category of Small n-fold Categories .
As far as I understand this “topological” Thomason-style model structure on Cat, 2Cat and cubical -cat is different from the “folklore” Lack-style model structure on Cat, 2Cat and that I think I am interested in.