A Wrinkle in the Mathematical Universe
Posted by John Baez
Of all the permutation groups, only has an outer automorphism. This puts a kind of ‘wrinkle’ in the fabric of mathematics, which would be nice to explore using category theory.
For starters, let be the groupoid of -element sets and bijections between these. Only for is there an equivalence from this groupoid to itself that isn’t naturally isomorphic to the identity!
This is just another way to say that only has an outer isomorphism.
And here’s another way to play with this idea:
Given any category , let be the category where objects are equivalences and morphisms are natural isomorphisms between these. This is like a group, since composition gives a functor
which acts like the multiplication in a group. It’s like the symmetry group of . But it’s not a group: it’s a ‘2-group’, or categorical group. It’s called the automorphism 2-group of .
By calling it a 2-group, I mean that is a monoidal category where all objects have weak inverses with respect to the tensor product, and all morphisms are invertible. Any pointed space has a fundamental 2-group, and this sets up a correspondence between 2-groups and connected pointed homotopy 2-types. So, topologists can have some fun with 2-groups!
Now consider , the groupoid of -element sets and bijections between them. Up to equivalence, we can describe as follows. The objects are just automorphisms of , while a morphism from an automorphism to an automorphism is an element that conjugates one automorphism to give the other:
So, if all automorphisms of are inner, all objects of are isomorphic to the unit object, and thus to each other.
Puzzle 1. For , all automorphisms of are inner. What are the connected pointed homotopy 2-types corresponding to in these cases?
Puzzle 2. The permutation group has an outer automorphism of order 2, and indeed What is the connected pointed homotopy 2-type corresponding to ?
Puzzle 3. Let be the groupoid where objects are finite sets and morphisms are bijections. is the coproduct of all the groupoids where :
Give a concrete description of the 2-group , up to equivalence. What is the corresponding pointed connected homotopy 2-type?
You can get a bit of intuition for the outer automorphism of using something called the Tutte–Coxeter graph.
Let . Of course the symmetric group acts on , but James Sylvester found a different action of on a 6-element set, which in turn gives an outer automorphism of .
To do this, he made the following definitions:
• A duad is a 2-element subset of . Note that there are duads.
• A syntheme is a set of 3 duads forming a partition of . There are also 15 synthemes.
• A synthematic total is a set of 5 synthemes partitioning the set of 15 duads. There are 6 synthematic totals.
Any permutation of gives a permutation of the set of synthematic totals, so we obtain an action of on . Choosing any bijection betweeen and , this in turn gives an action of on , and thus a homomorphism from to itself. Sylvester showed that this is an outer automorphism!
There’s a way to draw this situation. It’s a bit tricky, but Greg Egan has kindly done it:
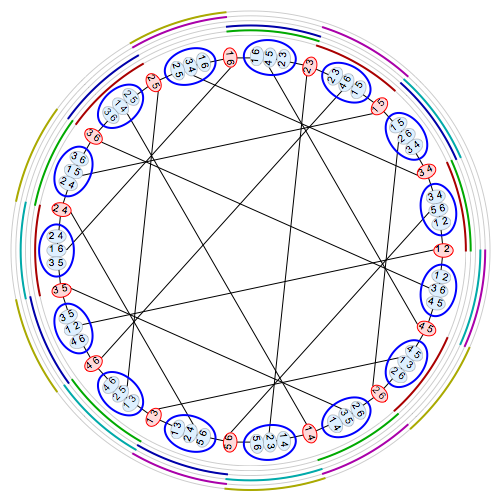
Here we see 15 small red blobs: these are the duads. We also see 15 larger blue blobs: these are the synthemes. We draw an edge from a duad to a syntheme whenever that duad lies in that syntheme. The result is a graph called the Tutte–Coxeter graph, with 30 vertices and 45 edges.
The 6 concentric rings around the picture are the 6 synthematic totals. A band of color appears in one of these rings near some syntheme if that syntheme is part of that synthematic total.
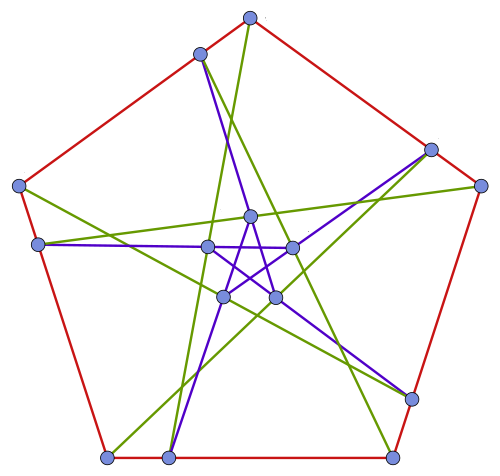
If we draw the Tutte–Coxeter graph without all the decorations, it looks like this:

The red vertices come from duads, the blue ones from synthemes. The outer automorphism of gives a symmetry of the Tutte–Coxeter graph that switches the red and blue vertices!
The inner automorphisms, which correspond to elements of , also give symmetries: for each element of , the Tutte–Coxeter graph has a symmetry that permutes the numbers in the picture. These symmetries map red vertices to red ones and blue vertices to blue ones.
The group has
elements, coming from the inner automorphisms of and the outer automorphism of order 2. In fact, is the whole symmetry group of the Tutte–Coxeter graph.
For more on the Tutte–Coxeter graph, see my post on the AMS-hosted blog Visual Insight:



Re: A Wrinkle in the Mathematical Universe
That got me trying to remember why the center of for is trivial. I remember learning something along the lines of the first of the answers given here.