A Survey of Magnitude
Posted by Tom Leinster
The notion of the magnitude of a metric space was born on this blog. It’s a real-valued invariant of metric spaces, and it came about as a special case of a general definition of the magnitude of an enriched category (using Lawvere’s amazing observation that metric spaces are usefully viewed as a certain kind of enriched category).
Anyone who’s been reading this blog for a while has witnessed the growing-up of magnitude, with all the attendant questions, confusions, misconceptions and mess. (There’s an incomplete list of past posts here.) Parents of grown-up children are apt to forget that their offspring are no longer helpless kids, when in fact they have a mortgage and children of their own. In the same way, it would be easy for long-time readers to have the impression that the theory of magnitude is still at the stage of resolving the basic questions.
Certainly there’s still a great deal we don’t know. But by now there’s also lots we do know, so Mark Meckes and I recently wrote a survey paper:
Tom Leinster and Mark Meckes, The magnitude of a metric space: from category theory to geometric measure theory. ArXiv:1606.00095; also to appear in Nicola Gigli (ed.), Measure Theory in Non-Smooth Spaces, de Gruyter Open.
Here I’ll tell you some of the highlights: ten things we used not to know, but do now.
Before I give you the highlights, I can’t resist repeating the definition of magnitude, as it’s so very simple.
Let be a finite metric space. Denote by the square matrix whose rows and columns are indexed by the points of , and with entries . Assuming that is invertible, the magnitude of is
— the sum of all the entries of the inverse matrix .
This definition immediately prompts the questions: why should be invertible? And how do you define magnitude for metric spaces that aren’t finite? The answers appear right at the beginning of the list below.
So, here are ten things we now know about magnitude that once upon a time we didn’t. They’re all covered in the survey paper, where you can also find references.
Magnitude is well-defined (that is, is invertible) for every finite subset of Euclidean space. In fact, is not only invertible but positive definite when .
There is a canonical way to extend the definition of magnitude from finite spaces to compact spaces, as long as they’re “positive definite” (meaning that the matrix is positive definite for every finite subset ). For instance, this includes all compact subspaces of .
What I mean by “canonical” is that there are several different ways that you might think of extending the definition, and they all give the same answer. For instance, you might define the magnitude of a compact positive definite space as the supremum of the magnitudes of its finite subsets. Or, you might take some sequence of finite subsets of whose union is dense in , “define” , and hope that none of the many things that could go wrong with this “definition” do go wrong. Or, you might abandon finite approximations altogether and try to take a more direct, analysis-based approach. Mark showed that these approaches all work and all give the same number.
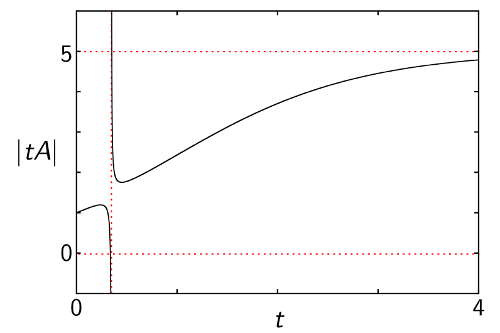
When you introduce a scale factor , the magnitude of a compact set is a continuous function of , taking values in (assuming ). This is called the magnitude function of .
The magnitude function of any finite metric space knows its cardinality. In fact, it is increasing for sufficiently large and converges to the cardinality as . This illustrates the idea that the magnitude of a finite space is the “effective number of points”.
The magnitude function of a compact subset of knows its volume. Specifically, Juan-Antonio Barceló and Tony Carbery showed that for compact ,
where is a known constant.
The magnitude function of a compact subset of also knows its Minkowski dimension. (Minkowski dimension is one of the more important notions of fractional dimension; it’s typically equal to the Hausdorff dimension.) Specifically, Mark showed that the Minkowski dimension of a compact set is equal to the growth of the magnitude function, meaning that there are constants such that
for all .
There’s an exact formula for the magnitude of the sphere of any dimension, with the geodesic metric. This was found by Simon Willerton.
There’s also an exact formula for the magnitude of any odd-dimensional Euclidean ball, computed by Barceló and Carbery. This formula raises lots of interesting questions, and I may say more about it in a future post.
The magnitude function of a convex body in with the taxicab metric (i.e. the metric induced by the 1-norm) is a polynomial. Its degree is the dimension of the body, and the coefficients are certain geometric measures of the body — e.g. up to a known factor, the top coefficient is the volume.
There are various asymptotic formulas for the magnitude functions of other spaces. For instance, Simon showed that the magnitude function of a homogeneous Riemannian -manifold is asymptotically a polynomial of degree whose top coefficient is proportional to the volume and whose th coefficient is proportional to the total scalar curvature. And Simon and I found various instances in which an asymptotic inclusion-exclusion principle holds: e.g. for the ternary Cantor set ,
corresponding to the fact that is the disjoint union of 2 copies of .
You can find more highlights, plus all the details I’ve left out, in our survey.
There are also a couple of important developments that we don’t cover:
The magnitude of a graph, and the corresponding homology theory. You can view a graph as a metric space: the points are the vertices, and distances are shortest path-lengths, giving all edges length . The study of magnitude for graphs has a special flavour, largely because distances in graphs are always integers. But most excitingly, it is just the shadow of a graded homology theory for graphs, developed by Richard Hepworth and Simon Willerton. Magnitude is the Euler characteristic of that homology theory, in the same way that the Jones polynomial is the Euler characteristic of Khovanov homology for links. For instance, the product formula for magnitude is a corollary of a Künneth theorem in homology — a decategorification of it, if you like. Similarly, a certain inclusion-exclusion formula for magnitude is the decategorification of a Mayer-Vietoris theorem for magnitude homology.
There is an intimate connection between magnitude and maximum entropy — or more exactly, the exponential of entropy, which I like to call diversity. Mark and I wrote this up separately a little while ago. In fact, Mark used the relationship between magnitude and maximum diversity to prove the result on Minkowski dimension that I mentioned earlier.
Incidentally, I know of just one other categorically-minded paper with the words “geometric measure theory” in the title, and it’s one of my favourite papers of all time:
Stephen H. Schanuel, What is the length of a potato? An introduction to geometric measure theory. In Categories in Continuum Physics, Lecture Notes in Mathematics 1174. Springer, Berlin, 1986.
It’s nine pages of pure joy. Even if you don’t read our survey, I strongly recommend that you read this!

Re: A Survey of Magnitude
Cool stuff!
I’m curious: Some finite metric spaces can’t be isometrically embedded in a Euclidean space. Is there a known example of a finite metric space for which is not invertible?