Random Permutations (Part 12)
Posted by John Baez
This time I’d like to repackage some of the results in Part 11 in a prettier way. I’ll describe the groupoid of ‘finite sets equipped with a permutation’ in terms of Young diagrams and cyclic groups. Taking groupoid cardinalities, this description will give a well-known formula for the probability that a random permutation belongs to any given conjugacy class!
Here is what we’ll prove:
Let me explain the notation here.
First, stands for the groupoid of finite sets equipped with permutation. Explicitly:
- an object of is a finite set with a bijection ;
- a morphism is a bijection such that .
Second, stands for the set of Young diagrams. A Young diagram looks like this:
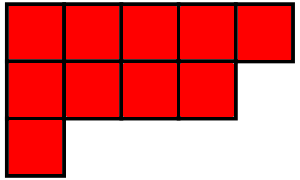
but we will think of Young diagrams as functions that vanish at all but finitely many points. The idea is that a Young diagram has columns of length for each . For example, the Young diagram above has and for all other .
Third, stands for the one-object groupoid corresponding to the group .
Fourth, for any category ,
stands for the th symmetrized power of . This is easiest to understand if we recall that the free symmetric monoidal category on , say , has a description as
where an object of is a -tuple of objects of and a morphism is a -tuple of morphisms in together with a permutation . The morphisms are composed in a manner familiar from the ‘wreath product’ of groups. Indeed, if is a group and is the corresponding one-object groupoid, we have
where the semidirect product is called the wreath product of and .
Now that all the notation is defined, we can prove the result:
Theorem. There is an equivalence of groupoids
Proof. First note that is equivalent to its full subcategory where we use one finite set with each cardinality. It is thus equivalent to the groupoid where
- an object is a natural number and an element ,
- a morphism is a permutation such that .
Thus, isomorphism classes of objects in correspond to conjugacy classes of permutations. A conjugacy class of permutations is classified by its number of cycles of each length, and thus by a Young diagram saying that there are cycles of length for each .
In short, if we use to stand for the set of isomorphism classes of objects of the groupoid , we have established an isomorphism
where is the set of Young diagrams. The groupoid is thus equivalent to a coproduct of connected groupoids, one for each Young diagram:
By taking a skeleton we can assume each groupoid has one object, namely where is a chosen permutation with cycles of length for each . The automorphisms of this object are then permutations with .
In short, is the one-object groupoid corresponding to the centralizer of , where is any permutation with cycles of length for all .
We can choose to act on the boxes of the Young diagram , cyclically permuting the entries in each column in such a way that the first entry in each column is mapped to the second, the second is mapped to the third, and so on, with the last entry being mapped to the first. Any element of the centralizer of thus consists of a permutation of the columns, mapping each column to some other column of the same height, followed by an arbitrary cyclic permutation of the entries in each column. It follows that the centralizer is isomorphic to
so
Then, by equation (1) and the fact that preserves products, we have
It follows that
as desired. ■
Now let’s see how this result lets us compute the probability that a random permutation of an -element set lies in any given conjugacy class. The conjugacy classes in correspond to Young diagrams with boxes. For each such we will compute the probability that a random element of lies in the corresponding conjugacy class. Let’s call this probability .
In general, the probability that a randomly chosen element of a finite group lies in some conjugacy class is . But where is the centralizer of some element . Thus, the probability in question equals .
Recall that is one-object groupoid corresponding to the centralizer of some whose conjugacy class corresponds to the Young diagram . The cardinality of a one-object groupoid is the reciprocal of the cardinality of the corresponding group, so
It follows that
In other words, the probability we are trying to compute is the cardinality of a groupoid we have already studied! We saw in the proof of the Theorem that
so
So, we get a well-known result:
Theorem. The probability that a random permutation of an -element set has cycles of length for all is given by
The theorem is easy to prove, so the point is just that this probability is the cardinality of a naturally defined groupoid, and a similar formula holds at the level of groupoids:
Here is the series so far, on my website:
- Part 0 — What’s the average length of the longest cycle in a random permutation of an -element set?
- Part 1 — What is the probability that a randomly chosen permutation of an -element set has exactly fixed points?
- Part 2 — What is the probability that the shortest cycle in a randomly chosen permutation of an -element set has length greater than ?
- Part 3 — A large collection of questions about random permutations, with answers.
- Part 4 — What is the probability that a randomly chosen permutation of an -element set has a cycle of length greater than ?
- Part 5 — What is the average length of a cycle in a randomly chosen permutation of an -element set?
- Part 6 — What expected number of cycles of length in a randomly chosen permutation of an -element set?
- Part 7 — How is the distribution of the number of cycles of length in a random permutation related to a Poisson distribution?
- Part 8 — What’s the th moment of a Poisson distribution?
- Part 9 — If we treat the number of cycles of length in a random permutation of an -element set as a random variable, what do the moments of this random variable approach as ?
- Part 10 — How to compute statistics of random permutations using groupoid cardinalities.
- Part 11 — How to prove the Cycle Length Lemma, a fundamental result on random permutations, using groupoid cardinalities.
- Part 12 — How to write the groupoid of finite sets equipped with a permutation as a sum over Young diagrams, and how to use this to compute the probability that a random permutation has given cycle lengths.

Re: Random Permutations (Part 12)
A gorgeous piece of objective mathematics! As this whole series has been.