Large Sets 5
Posted by Tom Leinster
Previously: Part 4. Next: Part 6
Last time, we met the “index” of an infinite set , which is the well-ordered set
It cannot be proved in ETCS that every well-ordered set is the index of some infinite set . However, if such an does exist, it’s unique for (up to isomorphism). It’s called : aleph-.
To recap, we saw that the process of taking the index defines an order-embedding
So
and therefore
So if a well-ordered set is isomorphic to for some infinite set , then is determined uniquely up to isomorphism, and we write . In that case, I’ll say exists.
For natural numbers , there’s exactly one well-ordered set with elements; call it . We write as . For example:
is the unique infinite set whose index is the empty well-ordered set ; that is, .
is the unique infinite set whose index is the one-element well-ordered set . That is, up to isomorphism, there is exactly one infinite set smaller than . So is , the smallest set .
The assignments and are mutually inverse:
for infinite sets , and
for well-ordered sets such that exists. Set theory books sometimes contain the statement “every infinite set is an aleph”; the first of these isomorphisms is our version of this.
For want of a better word, let’s say that a well-ordered set is alephable if exists. Then the inverse processes and define an equivalence
ZFC-based set theory puts the emphasis on the right-to-left assignment, . In ZFC, every well-ordered set is alephable, so that’s a reasonable thing to do. But in ETCS, where that’s not guaranteed, it makes more sense to emphasize the left-to-right direction, . That’s why I started there.
I chose the word “index” as an abbreviation for “aleph-index”: the index of is the well-ordered set such that . Maybe set theorists have no name for “index” because they’d just say “the ordinal such that ”.
Incidentally, the reason why I switched from to near the start of the last post was exactly so that we’d get an inverse to . I’d have been happy to stick with (thus, also including the finite sets ) if there was a standard name for the inverse to . That inverse would be a ladder of sets like the alephs, but starting at rather than . But as far as I know, it doesn’t have a name (and in particular, it’s not quite the same as the von Neumann hierarchy).
Which well-ordered sets are alephable? This is the same as the question “which well-ordered sets are the index of some set?”, which we already answered last time. Translating into the language of alephs, we know:
is alephable (i.e. exists);
if is alephable then so is , and ;
if is alephable then so is for all .
The first two properties guarantee that exists for all natural numbers . But need not exist for all well-ordered sets . In particular:
It is consistent with ETCS that does not exist.
This is just a restatement of a fact we met last time: it is consistent with ETCS that there is no set with index . What it tells us that if there are any models of ETCS at all, there is one in which the only sets are
That’s it. No more!
There’s a crucial characterization of the alephs that doesn’t mention index:
If exists, then so does for every , and is the smallest set for every .
For example, if exists then it is the smallest set with the property that for every .
To see why this characterization holds, think about the order-equivalence
We know that among all well-ordered sets, the alephable ones are downwards closed. Now, it’s a triviality that any well-ordered set is the least well-ordered set for every . Transporting this trivial fact across the equivalence, from right to left, gives the characterization of .
When people choose to denote a set by rather than just or whatever, it’s usually because they want to see it as part of the succession of alephs
The beginning part of that succession of alephs is displayed in what I called the “tautological bundle”. Last time I drew this picture for a set , where the fibre over an isomorphism class is itself:

If instead we start with an alephable well-ordered set and put , the picture becomes this:
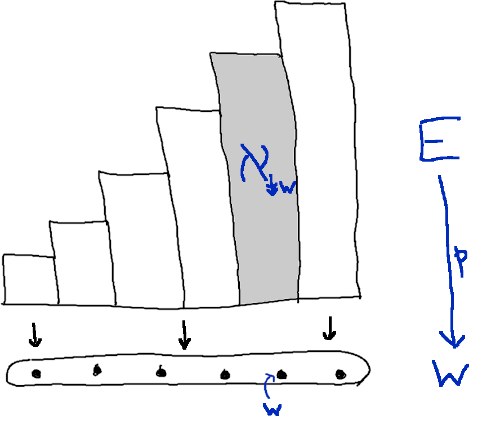
Here I’ve used the notation
when . It’s standard to write for the set of elements less than or equal to ; this is a variation on that notation. (If you want to use the double downwards arrow in the comments, I’m afraid the only way I know of getting it here is to use unicode: type “↡” without the quotation marks.)
Every downwards closed proper subset of is of the form for a unique . Equivalently, every well-ordered set is isomorphic to for a unique . So the fibres of are the alephs for .
The alephs that appear as the fibres here stop one short of itself. If we want to get as a fibre, we can do it by replacing by . Then the picture is:

Here I’ve lazily reused the letters and , which I shouldn’t really have done: they’re different from the and for . Anyway, the point is that the top fibre here is .
All this gives another characterization of the alephs. Let be a well-ordered set. Then exists if and only if there exist a set and function with the following property:
for all , the fibre is the smallest infinite set for all .
In that case, is determined uniquely up to isomorphism of sets over , and the fibre over the top element of is .
Summarizing what we’ve just seen and what we saw at the end of the last post, the following conditions on a model of ETCS are equivalent:
all alephs exist;
every well-ordered set is the index of some set;
the “Cantorian axiom”: for every well-ordered set , there exists a function into such that for all , the fibre is the smallest infinite set for all ;
for every set , there exists a function into whose fibres are pairwise non-isomorphic.
I’ll finish by relating the condition “all alephs exist” to the existence of limits (which we met in Part 2). First:
All alephs exist implies unboundedly many weak limits.
“Unboundedly many” means that for every set , there is some weak limit at least as big as .
Why is this true, assuming all alephs exist?
Let be an infinite set. We can take an initial well-ordered set with underlying set . I claim that does the job: that it’s a weak limit .
First, is a weak limit. “Initial” means that is the least well-ordered set of its cardinality, so can’t be a successor. Hence is a limit (as a well-ordered set). Now we saw last time that a set is a weak limit if and only if its index is a limit. Put another way, is a weak limit if and only if is a limit, for well-ordered sets . So is a weak limit.
All we have left to do is to show that . By construction, the underlying set of is , so our task is to show that
This looks like this should be true by miles: after all, is much bigger than , and is vastly bigger than , and is dramatically bigger than , etc. In a couple of posts’ time, we’ll look in detail at the question of versus . In any case, the inequality we have to prove follows from the inequality mentioned near the start of the last post. I’m running out of steam now so I won’t explain how, but it only takes a couple of lines.
So, if all alephs exist then there are unboundedly many weak limits. What about the converse? It’s false:
It is consistent with ETCS + (there are unboundedly many weak limits) that not all alephs exist.
In other words, “all alephs exist” is strictly stronger than “there are unboundedly many weak limits”.
For the proof, I’ll want to talk not only about weak limits and alephs, but also strong limits and beths. So that’s going to have to wait until next time.
Next time
There are two standard ways to make a set bigger: take its successor or its power set . The alephs are what you get by starting with and repeatedly taking successors. The beths are what you get by starting with and repeatedly taking power sets. We’ll meet the beths next time.

Re: Large Sets 5
I like this very much! But one thing that you did not mention (at least explicitly): for the case of , this will be the fibre over the top element of . But is also the total space of the bundle over . So I guess for limit ordinals there should be a similar phenomenon. This seems to be another way to state that exists.
Also, it’s trivial, but worth pointing out that in your last dot point in the list of things equivalent to the existence of all alephs (“function into ”), there’s an “off-by-” effect. When quantifying over all it’s invisible. But if one wants to get a specific then needs to either be bigger than by an initial copy of , or one must specify the fibres of the function to should be infinite.
(I’m being super picky, I know! But thinking of the pedagogical effect of these posts for people less used to axiomatic set theory)