The n-Category Café

Enriched categories

We get the notion of an enriched category by first considering the following definition of category. (Actually, it’s a definition of locally small category as it requires that the morphisms between a pair of objects form a set rather than anything bigger.) Here we will switch notation for hom-sets, moving from $\operatorname{Hom}_{\mathbf{\mathcal{C}}}(c, c')$ to the category theorists’ ${\mathbf{\mathcal{C}}}(c, c')$.

Definition 1. A category consists of a collection of objects, $\operatorname{Ob}{\mathbf{\mathcal{C}}}$, together with the following data which is required to satisfy the unit and associativity axioms:

(i) for all $c, c'\in \operatorname{Ob}{\mathbf{\mathcal{C}}}$ there is a specified set $${\mathbf{\mathcal{C}}}(c, c') \in \operatorname{Ob}{\mathbf{\mathcal{S}et}};$$

(ii) for all $c, c', c''\in \operatorname{Ob}{\mathbf{\mathcal{C}}}$ there is a specified function between sets $${\mathbf{\mathcal{C}}}(c, c') \times {\mathbf{\mathcal{C}}}(c', c'') \to {\mathbf{\mathcal{C}}}(c, c'');$$

(iii) for all $c \in \operatorname{Ob}{\mathbf{\mathcal{C}}}$ there is a specified element $\operatorname{id}_c\in {\mathbf{\mathcal{C}}}(c, c)$ which we can consider as a specified function $$\operatorname{id}_c\colon \{\ast\} \to {\mathbf{\mathcal{C}}}(c, c).$$

We obtain the defintion of enriched category by simply replacing the references to the monoidal category $({\mathbf{\mathcal{S}et}}, \times, \{\ast\})$ with references to the monoidal category $({\mathbf{\mathcal{V}}}, \otimes, \mathbb{1})$ that we are using as our base category.

Definition 2. A category enriched over ${\mathbf{\mathcal{V}}}$, or simply a ${\mathbf{\mathcal{V}}}$-category, consists of a collection of objects, $\operatorname{Ob}{\mathbf{\mathcal{C}}}$, together with the following data which is required to satisfy unit and associativity axioms:

(i) for all $c, c'\in \operatorname{Ob}{\mathbf{\mathcal{C}}}$ there is a specified object $${\mathbf{\mathcal{C}}}(c, c') \in \operatorname{Ob}{\mathbf{\mathcal{V}}};$$

(ii) for all $c, c', c''\in \operatorname{Ob}{\mathbf{\mathcal{C}}}$ there is a specified morphism in ${\mathbf{\mathcal{V}}}$ $${\mathbf{\mathcal{C}}}(c, c') \otimes {\mathbf{\mathcal{C}}}(c', c'') \to {\mathbf{\mathcal{C}}}(c, c'');$$

(iii) for all $c \in \operatorname{Ob}{\mathbf{\mathcal{C}}}$ there is a specified morphism in ${\mathbf{\mathcal{V}}}$ $$\operatorname{id}_c\colon \mathbb{1}\to {\mathbf{\mathcal{C}}}(c, c).$$

If you take ${\mathbf{\mathcal{V}}}$ to be the category of vector spaces ${\mathbf{\mathcal{V}ect}}$ then you see that a ${\mathbf{\mathcal{V}ect}}$-category is like a category except the ‘hom-sets’ are actually vector spaces and the composition maps are bilinear. The identity morphism in ${\mathbf{\mathcal{C}}}(c, c)$ is recovered by taking $\operatorname{id}_c(1)$ where $1\in \mathbb{C}$ means the unit complex number. For instance, for an algebra $A$, there is the one-object ${\mathbf{\mathcal{V}ect}}$-category ${\mathbf{\mathcal{B}}}A$ and the ${\mathbf{\mathcal{V}ect}}$-category ${\mathbf{\mathcal{R}ep}}(A)$ of $A$-representations.

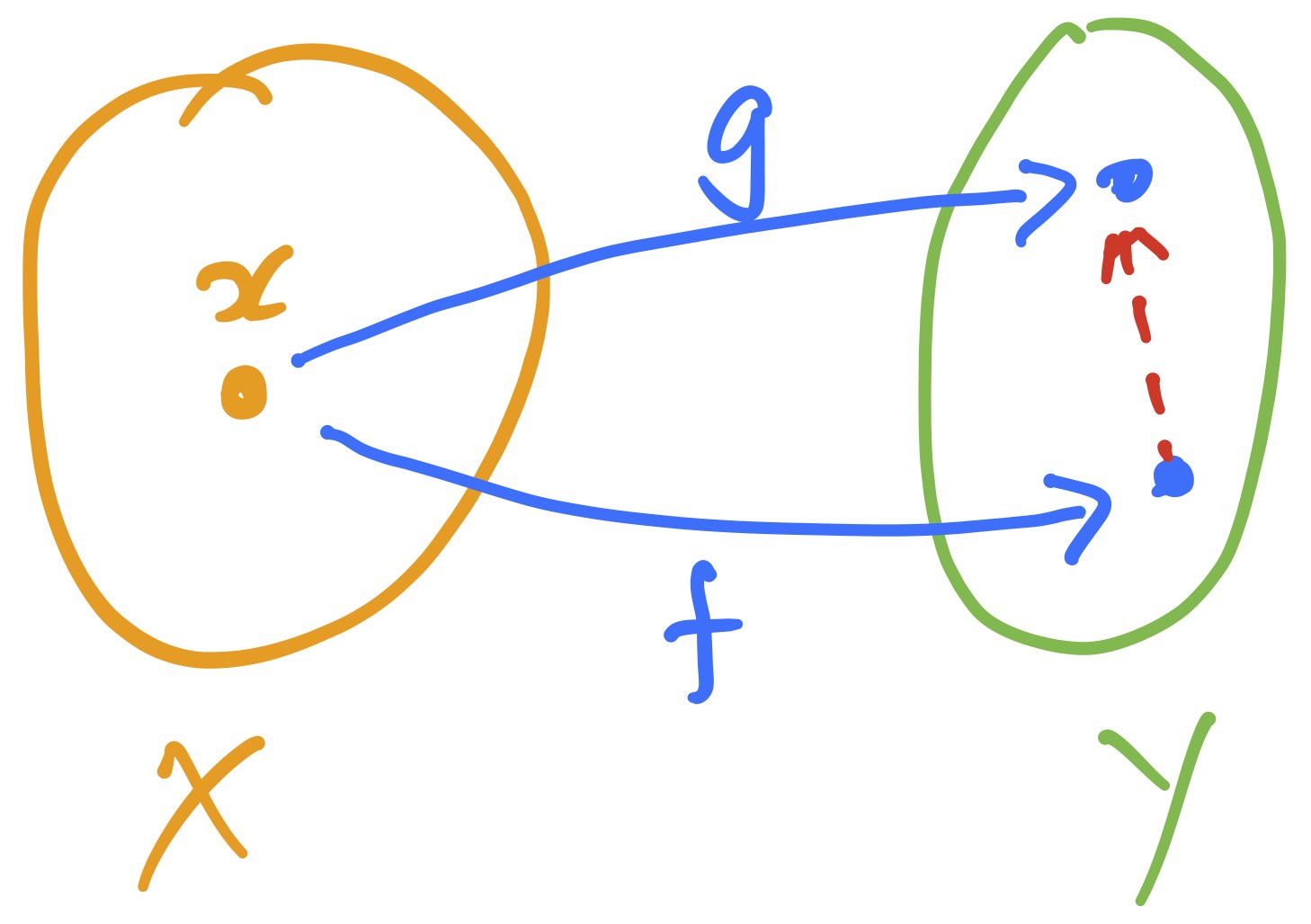
There is an accompanying notion of ${\mathbf{\mathcal{V}}}$-functor between ${\mathbf{\mathcal{V}}}$-categories.

Definition 3. For ${\mathbf{\mathcal{V}}}$-categories ${\mathbf{\mathcal{C}}}$ and ${\mathbf{\mathcal{D}}}$, a ${\mathbf{\mathcal{V}}}$-functor $F\colon {\mathbf{\mathcal{C}}}\to {\mathbf{\mathcal{D}}}$ consists of a function $F\colon \operatorname{Ob}{\mathbf{\mathcal{C}}}\to \operatorname{Ob}{\mathbf{\mathcal{D}}}$ and for each pair $c,c'\in \operatorname{Ob}{\mathbf{\mathcal{C}}}$ a specified morphism ${\mathbf{\mathcal{C}}}(c, c') \to {\mathbf{\mathcal{D}}}(F(c), F(c'))$ in ${\mathbf{\mathcal{V}}}$. These are required to satisfy composition and unit axioms.

In particular, a ${\mathbf{\mathcal{V}ect}}$-functor is required to be given by linear maps between the hom-spaces.

The nicer that the enriching category ${\mathbf{\mathcal{V}}}$ is, the nicer that the theory of ${\mathbf{\mathcal{V}}}$-categories is. I won’t go into detail here, but in particular, we have the following.

• If ${\mathbf{\mathcal{V}}}$ is so-called closed monoidal then you can make ${\mathbf{\mathcal{V}}}$ into a ${\mathbf{\mathcal{V}}}$-category itself, analogous to how you can make a ring into a module over itself.

• If ${\mathbf{\mathcal{V}}}$ is braided (in particular if it is symmetric) so that there are natural and coherent isomorphisms $v_1 \otimes v_2 \cong \v_2 \otimes v_1$ for $v_1, v_2 \in {\mathbf{\mathcal{V}}}$, then for a pair of ${\mathbf{\mathcal{V}}}$-categories ${\mathbf{\mathcal{C}}}$ and ${\mathbf{\mathcal{D}}}$ you can form the tensor product ${\mathbf{\mathcal{V}}}$-category ${\mathbf{\mathcal{C}}}\otimes {\mathbf{\mathcal{D}}}$, analogous to how you can take tensor product of modules for commutative rings.

• If ${\mathbf{\mathcal{V}}}$ has sufficiently many limits then for a pair of ${\mathbf{\mathcal{V}}}$-categories ${\mathbf{\mathcal{C}}}$ and ${\mathbf{\mathcal{D}}}$ you can form the functor ${\mathbf{\mathcal{V}}}$-category $[{\mathbf{\mathcal{C}}}, {\mathbf{\mathcal{D}}}]$ where the objects are ${\mathbf{\mathcal{V}}}$-functors of the form $F\colon {\mathbf{\mathcal{C}}}\to {\mathbf{\mathcal{D}}}$. (There can be size issues here if $C$ is not sufficiently small.)

In many cases of interest the enriching category ${\mathbf{\mathcal{V}}}$ is braided closed monoidal with sufficiently many limits, so a small ${\mathbf{\mathcal{V}}}$-category ${\mathbf{\mathcal{C}}}$ has a ${\mathbf{\mathcal{V}}}$-category $[{\mathbf{\mathcal{C}}}, {\mathbf{\mathcal{V}}}]$ of scalar-valued functors, or presheafs, on ${\mathbf{\mathcal{C}}}$.

For instance, for an algebra $A$, the ${\mathbf{\mathcal{V}ect}}$-category ${\mathbf{\mathcal{R}ep}}(A)$ of representations of $A$ can be given as the functor category on ${\mathbf{\mathcal{B}}}A$:

$${\mathbf{\mathcal{R}ep}}_A = [{\mathbf{\mathcal{B}}}A, {\mathbf{\mathcal{V}ect}}].$$

This is what we were hoping for above.

Metric spaces as $\overline{\mathbb{R}}_{+}$-categories

If we enrich over the monoidal category $\overline{\mathbb{R}}_{+}$ of extended non-negative real numbers then we can simplify the general definition a little and get the following.

Definition 4. An $\overline{\mathbb{R}}_{+}$-category, consists of a collection of objects, $\operatorname{Ob}X$, together with the following data:

(i) for all $x, x'\in \operatorname{Ob}X$ there is a specified number $$X(x, x') \in [0,\infty];$$

(ii) for all $x, x', x''\in \operatorname{Ob}X$ there is an inequality $$X(x, x') + X(x', x'') \ge X(x, x'');$$

(iii) for all $x \in \operatorname{Ob}X$ there is an equality $$0 = X(x, x).$$

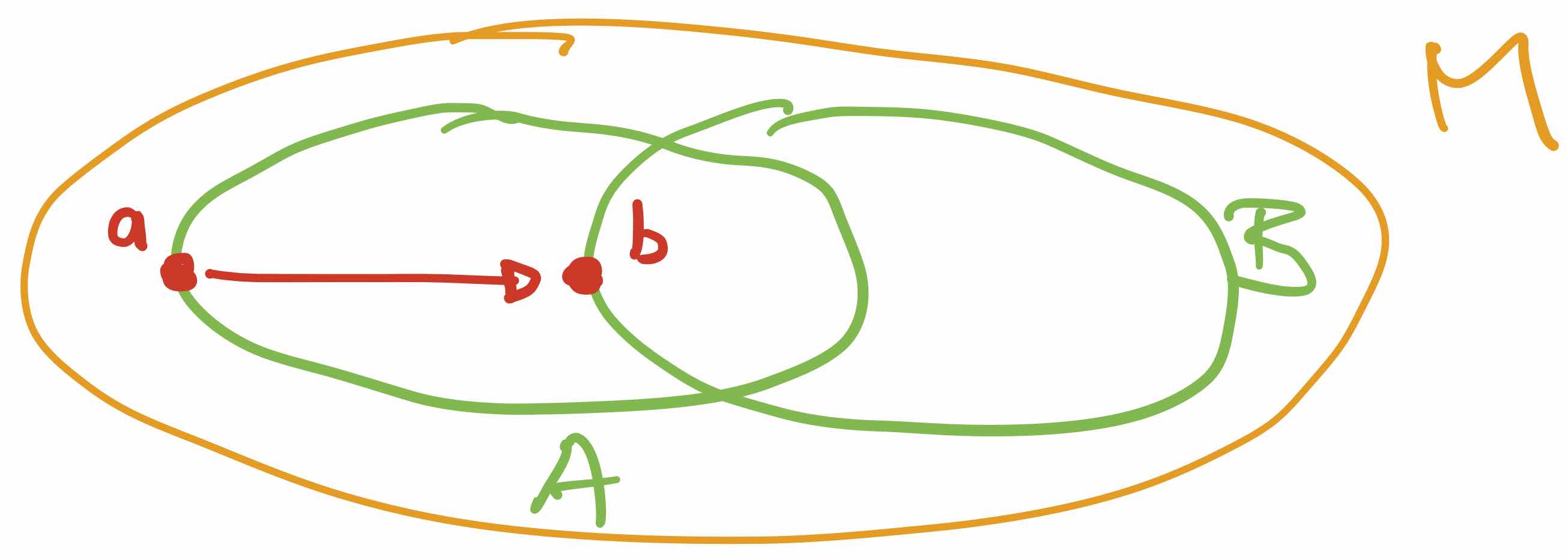
There are several things to note here. Firstly, because $\overline{\mathbb{R}}_{+}$ is a thin category, all diagrams commute so the associativity and unitality conditions are automatically satisfied and so do not need to be specified. Secondly, the “composition morphism” in (ii) is clearly a “triangle inequality”, so we can think of the hom-object $X(x, x')$ as a “distance” from $x$ to $x'$. Thirdly, from the definition of enriched category the “zero self-distance” in (iii) would be written as $0 \ge X(x, x)$ but as we know that the hom-object is non-negative, we can conclude the inequality is actually an equality.

If, as indicated above, we think of the hom-objects as being distances then we can think of a $\overline{\mathbb{R}}_{+}$-category as a kind of generalized metric space. The traditional notion of metric space was due to Fréchet: by contrast, $\overline{\mathbb{R}}_{+}$-categories are sometimes known as Lawvere metric spaces; these differ from Fréchet metric spaces in the following three ways.

1. The distance is not necessarily symmetric, so we allow $X(x, x') \ne X(x', x)$.

2. The distance between two points can be infinite.

3. The distance from one point to a different point can be zero.

We’ll see some examples illustrating these below.

From this generalized metric space perspective, an $\overline{\mathbb{R}}_{+}$-functor $f\colon X \to Y$ is viewed as a short map or distance non-increasing function, so it is a function $f\colon \operatorname{Ob}X \to \operatorname{Ob}Y$ such that $X(x, x') \ge Y\big(f(x), f(x')\big)$ for all $x, x' \in \operatorname{Ob}X$.

Here are the promised examples.

• We can equip $\overline{\mathbb{R}}_{+}$ with the structure of an $\overline{\mathbb{R}}_{+}$-category. This is basically the fact that $\overline{\mathbb{R}}_{+}$ is a closed monoidal category. It is a slight abuse of notation to refer to the category and the $\overline{\mathbb{R}}_{+}$-category as $\overline{\mathbb{R}}_{+}$ but it doesn’t usually cause confusion. Anyway we define the generalized metric as follows. $$\overline{\mathbb{R}}_{+}(a, b) = b  \stackrel{.}{-} a \coloneqq \max(b - a, 0).$$ The operation $ \stackrel{.}{-} $ is sometimes referred to as truncated subtraction. If we think of the extended non-negative real numbers as standing going upwards, then for $b \ge a$ we can think of it being ‘free’ to descend from $b$ to $a$, but having a ‘cost’ of $b-a$ associated with ascending from $a$ to $b$.

• As $\overline{\mathbb{R}}_{+}$ is sufficiently nice – it has all limits, which are given by suprema – if $X$ and $Y$ are $\overline{\mathbb{R}}_{+}$-categories then there is the functor $\overline{\mathbb{R}}_{+}$-category $[X, Y]$ consisting of short maps from $X$ to $Y$ and the generalized metric given as follows:

  $$[X, Y](f, g) \coloneqq\sup_{x\in X} Y(f(x), g(x)).$$

  

  This is a measurement of the furthest apart that $f$ and $g$ get. In particular, if we take $Y= \overline{\mathbb{R}}_{+}$ then we can get the following generalized metric on scalar-valued short maps: $$[X, \overline{\mathbb{R}}_{+}](f, g) \coloneqq\sup_{x\in X} \left(g(x)  \stackrel{.}{-} f(x)\right).$$

  The Yoneda embedding is an distance preserving (ie. isometric) function: $$X \hookrightarrow [X^{\mathrm{op}}, \overline{\mathbb{R}}_{+}]; \quad x \mapsto X({-}, x).$$ In the case of a classical metric space we have $X = X^\mathrm{op}$ as the distance is symmetric and the embedding in sometimes known as the Kuratowski embedding.

  We can see that this notion of generalized metric on function spaces is a refinement of the standard notion of ‘sup-metric’ on function spaces. If we look at all functions from the unit interval $I = \{x \mid 0 \le x \le 1\}$ to the set $\mathbb{R}_{\ge 0}$ then we can consider these as short maps from $I_\delta$ to $\overline{\mathbb{R}}_{+}$ where $I_\delta$ is the interval equipped with the discrete metric so that the distance $I(x, x')$ is $0$ if $x=x'$ and is $\infty$ otherwise. Then for functions $f, g\colon I\to \mathbb{R}_{\ge 0}$ we have that the sup-metric between them is a symmetrization of the enriched category metric: $$\begin{aligned}\textstyle\sup_x \left| f(x) - g(x) \right| &= \max\Bigl( \sup_x (g(x)  \stackrel{.}{-} f(x)), \sup_x (f(x)  \stackrel{.}{-} g(x))\Bigr)\\ &=\max\Bigl([I_\delta, \overline{\mathbb{R}}_{+}](f, g), [I_\delta, \overline{\mathbb{R}}_{+}](g, f)\Bigr). \end{aligned}$$

• Now we can see an example where even if we are just interested in classical metric spaces we naturally end up with an asymmetric metric, although it is usually symmetrized to obtain the Hausdorff metric! Given a classical metric space $M$ we can take the set of compact, non-empty subsets, $S_M \coloneqq\{A \subseteq M \mid A\ \text{compact},A\ne \emptyset\}$. We can then define a generalized metric on this by $$S_M(A, B) \coloneqq \sup_{a\in A}\inf_{b\in B} M(a, b).$$

  

  One way of thinking about $S_M(A, B)$ is that it is measuring the furthest you would have to go if you were dropped at a random point in $A$ and wanted to take the shortest route to $B$. Because we are considering compact sets we have the following simple characterization of zero-distance, which is telling us that the generalized metric is encoding the usual order on subsets: $$S_M(A, B) = 0 \quad \Longleftrightarrow \quad A \subseteq B.$$ (If we hadn’t used compact subsets then we wouldn’t have had such a nice characterization.) This leads us to see that this generalized metric is naturally asymmetric even though we started with a symmetric metric on $M$. The usual Hausdorff metric $\operatorname{d}_{\mathrm{H}}$ is obtained by symmetrizing this generalized metric: $$\operatorname{d}_{\mathrm{H}}(A, B) = \max\big(S_M(A, B), S_M(B, A)\big).$$ Clearly, however, the Hausdorff metric is losing information, such as the partial order, that was contained in the generalized metric.

This concludes the quick introduction to metric spaces as enriched categories. However, this perspective does allow other categorical techniques to be used with metric spaces, leading to some fruitful mathematics.

Afterword

It’s probably worth mentioning my experiences a little. As a Part III student at Cambridge, like many students before and after me, I attended Peter Johnstone’s Category Theory course, so I had familiarity with category theory, but, as I didn’t take the exam, I didn’t have a deep understanding. I then went on to do my PhD and later work on things related to algebraic topology and topological quantum field theory which both have strong categorical underpinnings. Coming back to the basics of category theory when I was involved in the Catsters with Eugenia Cheng I realised that various things didn’t chime with my experience of using categories and certain things seemed almost arcane to me, for example the importance put on things like monoids and functors into the category of sets.

It wasn’t until many, many years later that I started to understand that this cognitive dissonance was because in areas like algebraic topology, topological field theory, representation theory and algebraic geometry it is much more useful to consider that you’re not working over the category of sets but over some other category like vector space or abelian groups or chain complexes. As a ‘working mathematician’, rather than monoids and functors into the category of sets, I would have been much more familiar with algebras or rings and with functors into the category of vector spaces or abelian groups.

Although I was aware of the notion of enriched category theory, I didn’t get a thorough appreciation of quite what it meant until I’d spent a lot of time thinking about metric spaces in this context in particular via Lawvere’s rather wonderful paper Metric spaces, generalized logic and closed categories. I think one reason that enriched category is not more appreciated as a perspective is that the main text, Kelly’s Basic Concepts of Enriched Category Theory, is not particularly welcoming and only entered into by the brave! I could probably try to make the area more welcoming by polishing up my first attempt at a draft book on enriched categories, but with all of the other things I want to do, unfortunately I don’t see that happening too soon.