The n-Category Café

There’s an adjunction between commutative monoids and pointed sets. Any commutative monoid $(M,+,0)$ has an underlying pointed set $(M,0)$, so we get a functor

$$U : \mathsf{CommMon} \to \mathsf{Set}_\ast$$

from commutative monoids to pointed sets. And this has a left adjoint

$$F: \mathsf{Set}_\ast \to \mathsf{CommMon}$$

This sends any pointed set $(S,\ast)$ to the free commutative monoid on $S$ modulo the congruence relation that forces $\ast$ to be the identity. And that’s naturally isomorphic to the free commutative monoid on the set $S - \{\ast\}$.

So, we get a comonad

$$F U : \mathsf{CommMon} \to \mathsf{CommMon}$$

What happens if we start with our favorite 2-element commutative monoid, and repeatedly apply this comonad?

My favorite 2-element commutative monoid is the booleans $B = \{0,1\}$ made into a commutative monoid using ‘or’. Its identity element is $0$.

If we take $(B, or, 0)$ and apply the functor

$$U : \mathsf{CommMon} \to \mathsf{Set}_\ast$$

we get the 2-element pointed set $(B,0)$. When we apply the functor

$$F: \mathsf{Set}_\ast \to \mathsf{CommMon}$$

to this 2-element pointed set we get $\mathbb{N}$, made into a commutative monoid using addition. The reason is that $\mathbb{N}$ is also the free commutative monoid on the 1-element set $B - \{0\}$.

If we apply the functor $U$ to $(\mathbb{N}, + , 0)$ we get the pointed set $(\mathbb{N},0)$. When we apply the functor $F$ to the pointed set $(\mathbb{N},0)$ we get a commutative monoid that’s also the free commutative monoid on the set $\mathbb{N} - \{0\} = \{1,2,3,\dots\}$. This is usually called the set of Young diagrams, since a typical element looks like

$$3 + 2 + 2 + 2 + 1$$

so it can be drawn like this:

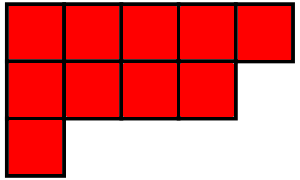
(I’m counting the number of boxes in columns. We can also use the other convention, where we count the number of boxes in rows. That’s actually more common.)

Note that there is an ‘empty Young diagram’ with no boxes at all, and that’s the identity element of the free commutative monoid on $\{1,2,3,\dots\}$. But there aren’t Young diagrams with a whole bunch of 0-box columns, which is why I prefer the free commutative monoid on $\{1,2,3,\dots\}$ to the free commutative monoid on $\mathbb{N}$.

Let $(Y,+,0)$ be the commutative monoid of Young diagrams, where $0$ is the empty Young diagram — the one with no boxes at all. Applying $U$ to this we get the pointed set of Young diagrams, $(Y,0)$. Applying $F$ to that we get a commutative monoid $F(Y,0)$ that’s also the free commutative monoid on the set of nonempty Young diagrams.

And this commutative monoid $F(Y,0)$ is important in representation theory! The category $\mathsf{Schur}$ of Schur functors has Young diagrams as its simple objects. But a general object is a finite direct sum of simple objects. So, the set of isomorphism classes of Schur functors is naturally isomorphic to $F(Y,0)$. And they are isomorphic as commutative monoids, where we use direct sums of Schur functors to get a monoid structure.

So here is the slogan:

Take the booleans, apply the comonad $F U$ and get the commutative monoid of natural numbers.

Take the natural numbers, apply the comonad $F U$ and get the commutative monoid of Young diagrams.

Take the Young diagrams, apply the comonad $F U$ and get the commutative monoid of isomorphism classes of Schur functors.

Of course I want to do it again, but I’m not sure where the resulting structure shows up in math. Maybe some sort of categorified representation theory?