Symmetric Spaces and the Tenfold Way
Posted by John Baez
I’ve finally figured out the really nice connection between Clifford algebra and symmetric spaces! I gave a talk about it, and you can watch a video.
I gave my talk in Nicohl Furey’s series Algebra, Particles and Quantum Theory on Monday May 15, 2023. This talk is a followup to an earlier talk, also about the tenfold way.
You can see a video of my new talk here and see my slides here. The slides have material on category theory that I didn’t get around to talking about.
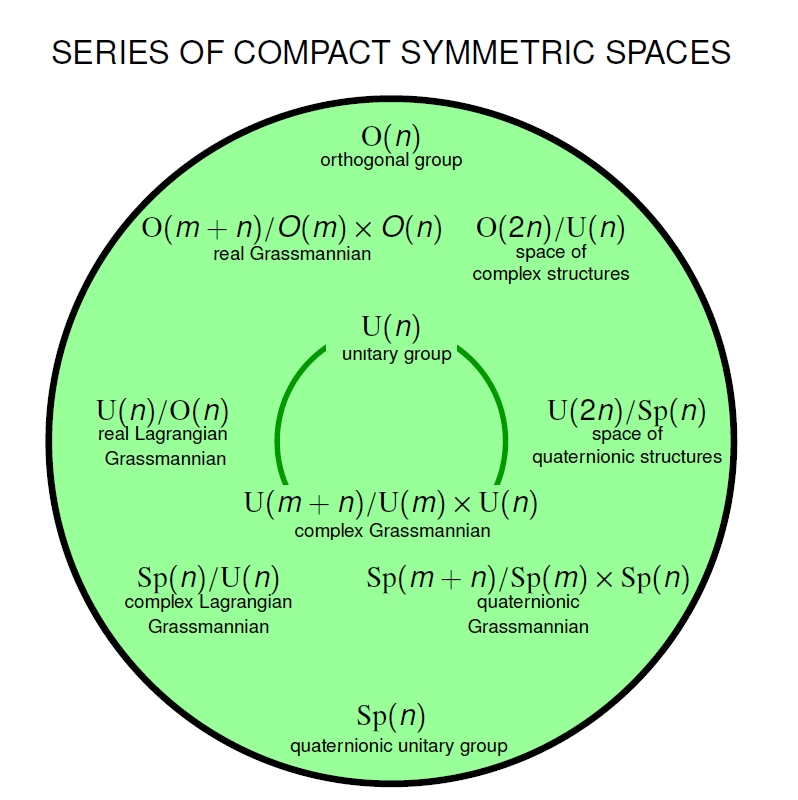
Abstract: The tenfold way has many manifestations. It began as a tenfold classification of states of matter based on their behavior under time reversal and charge conjugation. Mathematically, it relies on the fact that there are ten super division algebras and ten kinds of Clifford algebras, where two Clifford algebras are of the same kind if they have equivalent super-categories of super-representations. But Cartan also showed that there are ten infinite families of compact symmetric spaces! After explaining symmetric spaces, we show how they arise naturally from forgetful functors between categories of representations of Clifford algebras.
The final upshot is this:
Let the Clifford algebra be the free real or complex algebra on anticommuting square roots of . Let
be the forgetful functor between representation categories. Then the essential fibers of this functor are disjoint unions of compact symmetric spaces. Moreover we get all the compact symmetric spaces in the ten infinite families this way!
(There are also finitely many exceptional ones, which all arise from the octonions.)


U(g)
This sounds great! I had some questions straightaway, but I am beginning to find answers to them in the slides.
What are the ways to make a universal enveloping algebra U(g) a *-algebra?