The n-Category Café

Let’s try to get a clearer geometrical picture of what I’ve been talking about lately.

The algebra I’ll be discussing today works for any commutative algebra $A$ over any commutative ring $k$. And so does the geometry! The idea is to think of $A$ as an algebra of functions on some sort of space $X$. Algebraic geometers call this sort of space an affine scheme over $k$, and call $X$ the spectrum of $A$. But don’t let that intimidate you! I’ll draw pictures of very simple cases, like where $X$ is a line.

Since $A$ is the algebra of functions on $X$, $A \otimes A$ is the algebra of functions on $X \times X$. The idea is that given functions $f$ and $g$ on $X$ we get a function $f \otimes g$ on $X \times X$ by

$$(f \otimes g)(x,y) = f(x) g(y)$$

Notice, there are two different ways to multiply functions in $A \otimes A$ by functions on $A$. One is on the left:

$$f (g \otimes h) = f g \otimes h$$

This multiplies a function on $X \times X$ by a function that depends only on ‘$x$ coordinate’:

$$(f (g \otimes h))(x,y) = f(x) g(x) h(y)$$

The other is on the right:

$$(g \otimes h)f = g \otimes h f$$

This multiplies a function on $X \times X$ by a function that depends only on ‘$y$ coordinate’:

$$((g \otimes h)f)(x,y) = g(x) h(y) f(y)$$

This fact — that you can multiply functions on $A \otimes A$ by functions in $A$ in two ways, which obey nice associative laws — can be summarized by saying that $A \otimes A$ is an $A,A$-bimodule.

By the way, the term ‘$x$ and $y$ coordinates’ is a bit poetic here: a better thing to say might be ‘first and second variables’. But when $X$ is the real line, my picture of $X \times X$ is this:

                                   

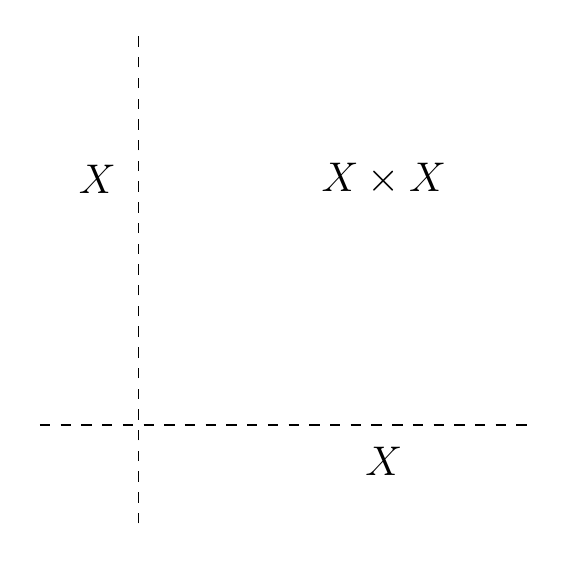
and in this example, $x$ and $y$ really are just the usual $x$ and $y$ coordinates.

Now, sitting inside $X \times X$ is the diagonal

$$D = \{(x,x) \; \vert \; x \in X\} \subseteq X \times X$$

This plays a starring role in all that follows, so please visualize it:

                                   

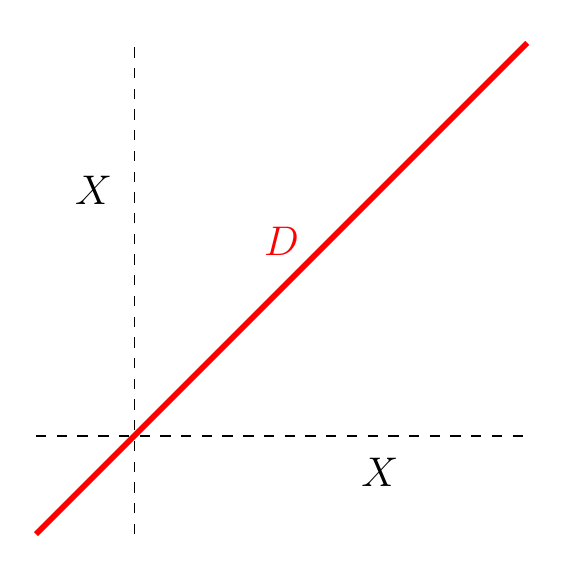
The functions vanishing on the diagonal form an ideal in $A \otimes A$. Let’s call it $I$. Algebraically, this ideal is precisely the kernel of the multiplication map

$$m \colon A \otimes A \to A$$

I wish this were more visually obvious to me, but it follows from the proof of Lemma 15.

The quotient ring $(A \otimes A)/I$ is the ring of functions on the diagonal. But of course, the diagonal is isomorphic to $X$ itself. So,

$$(A \otimes A)/I \; \cong \; A$$

We can dignify this fact by saying we’ve got a short exact sequence of $A,A$-bimodules:

$$0 \longrightarrow I \stackrel{i}{\longrightarrow} A \otimes A \stackrel{m}{\longrightarrow} A \to 0$$

where $i$ is the inclusion of the ideal $I$ in $A \otimes A$. Here $A$ is an $A,A$-bimodule where the left and right actions of $A$ agree. That makes sense, since on the diagonal we have $x = y$.

In Lemma 16 I pointed out something simple but important: the algebra $A$ is separable iff this short exact sequence splits! Concretely, this means there’s an $A,A$-bimodule homomorphism

$$p \colon A \otimes A \to I$$

such that $i \circ p$ is the identity. This implies the ideal $I$ is actually a commutative ring, since taking the unit $1 \in A \otimes A$ and applying $p$ to it we get a unit for $I$ — check it out! So, for a separable algebra $A$ we get a way of chopping up $A \otimes A$ like this:

$$A \otimes A \cong A \oplus I$$

not only as $A,A$-bimodules, but as commutative rings.

This means we can take the ring of functions on $X \otimes X$ and separate it into two parts that are themselves rings. One of them is $I$, the functions that vanish on the diagonal. The other is $A$, which is the functions that vanish off the diagonal.

And now we finally come to the main point:

The geometrical meaning of separability is that we can separate $X \times X$ into two disjoint pieces: the diagonal $D$ and the complement $X \times X - D$.

Yes, the word ‘separable’ actually means you can separate $X \times X$ into two pieces. I thank Tom Leinster for pointing this out to me. Finally the word makes sense.

Most commutative algebras are not separable. An affine scheme $X \times X$ is not usually the coproduct of the diagonal and ‘the rest’. The problem is that ‘the rest’ snuggles up arbitrarily close to the diagonal.

For example, in the world of affine schemes the plane is not the disjoint union of the diagonal line and the rest of the plane. So the pictures I’ve been showing so far do not illustrate the separable case.

Here’s an example of the separable case:

                                   

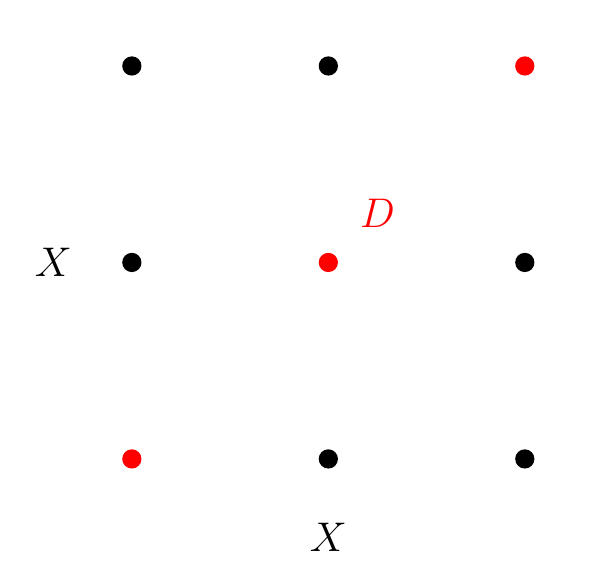
Now $X$ is just three points. $X \times X$ is all 9 points shown above. The diagonal $D$ is the red points, and the ‘rest’, $X \times X - D$, is the 6 black points. So $X \times X$ breaks cleanly into the diagonal and the rest.

All this is related to calculus in a great way. $(A \otimes A)/I^2$ consists of functions on $X \times X$ modulo functions that vanish to second order on the diagonal. In our example where $X$ is the real line, $A/I^2$ consists of Taylor series where we expand about the diagonal, like this:

$$f(x,y) = f(x,x) + \frac{\partial f(x,y)}{\partial x} (x - y) + \cdots$$

but then throw out all the higher order terms! You see, $x - y \in I$ so $(x - y)^2 \in I^2$, and in $A/I^2$ we set it to zero. We’re left with a first-order Taylor series of this form:

$$g(x) + h(x) (x - y)$$

Since $y - x$ is nonzero in $(A \otimes A)/I^2$ but its square is zero, it acts like an ‘infinitesimal’. This is part of a whole philosophy relating nilpotent elements of rings to infinitesimals.

In general, for any commutative algebra $A$, people call the affine scheme corresponding to $A/I^2$ is the ‘first-order infinitesimal neighborhood of the diagonal’ in $X \times X$. I visualize it sort of like this:

                                   

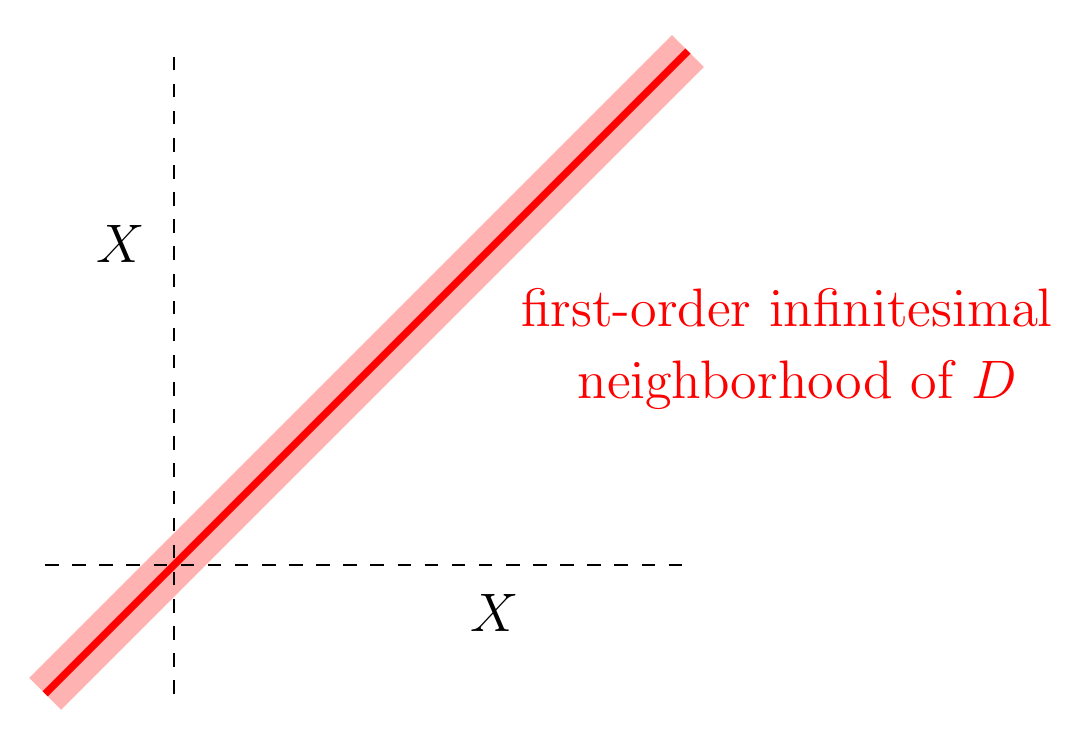
It’s hard to draw accurately, because it’s thicker than a line but only infinitesimally thicker. Algebraic geometers often call this sort of infinitesimal thickening ‘nilpotent fuzz’.

Next, what about $I/I^2$? This consists of functions on $X \times X$ that vanish on the diagonal modulo functions that vanish to second order on the diagonal. And these are the same as 1-forms on $X$, since they say to first order how a function changes as you start at a point $(x,x)$ and then start moving to a nearby point $(x,y)$.

But by ‘1-forms’, what I really mean are Kähler differentials, elements of $\Omega^1(A)$. I defined these in Part 3, and Lemma 15 proved that

$$I/I^2 \cong \Omega^1(A)$$

So, if what I’m saying now seems annoyingly hand-wavy, check that out.

What happens if $A$ is separable? First, the diagonal in $X \times X$ is the same as its own first-order infinitesimal neighborhood. There’s nothing ‘infinitesimally close’ to the diagonal except the diagonal itself! This is easy to believe in our example where $X$ is a finite set of points:

                                   

But it’s also rigorous math: if $A$ is separable then the ideal $I$ has a multiplicative unit, so $I = I^2$, and

$$(A \otimes A)/I^2 \; =\; (A \otimes A)/I \; \cong \; A$$

Second, if $A$ is separable there aren’t any nonzero 1-forms on $X$. More precisely:

$$\Omega^1(A) \cong I/I^2 \cong 0$$

This is a precise way of saying that the affine scheme $X$ is ‘zero-dimensional’.

So, much of what I’ve been doing has a nice geometrical meaning. Atiyah famously claimed:

Algebra is the offer made by the devil to the mathematician. The devil says: “I will give you this powerful machine, it will answer any question you like. All you need to do is give me your soul: give up geometry and you will have this marvellous machine.”

I don’t agree. To me there is insight to be had in algebra as well as geometry: it’s not just a “powerful machine”. But even if you agree with Atiyah, you can cheat the devil. You can compute using algebra, and then go back and interpret what you’ve done using geometry.

By the way, besides algebra and geometry there’s also logic. The diagonal $D \subset X \times X$ corresponds to the predicate $x = y$. If $X$ is the spectrum of a separable algebra, there’s also an affine scheme $X - D \subseteq X \times X$ corresponding to the predicate $x \ne y$, and a version of the ‘law of excluded middle’ holds.