Skip to the Main Content

Note:These pages make extensive use of the latest XHTML and CSS Standards. They ought to look great in any standards-compliant modern browser. Unfortunately, they will probably look horrible in older browsers, like Netscape 4.x and IE 4.x. Moreover, many posts use MathML, which is, currently only supported in Mozilla. My best suggestion (and you will thank me when surfing an ever-increasing number of sites on the web which have been crafted to use the new standards) is to upgrade to the latest version of your browser. If that's not possible, consider moving to the Standards-compliant and open-source Mozilla browser.

November 5, 2024

The Icosahedron as a Thurston Polyhedron

Posted by John Baez

Thurston gave a concrete procedure to construct triangulations of the 2-sphere where 5 or 6 triangles meet at each vertex. How can you get the icosahedron using this procedure?

Gerard Westendorp has a real knack for geometry, and here is his answer.

Here is Thurston’s procedure. First draw the lattice of Eisenstein integers in the complex plane:

𝔼={a+bω|a,b∈ℤ}\mathbb{E} = \{ a + b \omega \; \vert \; a, b \in \mathbb{Z} \}

where ω=exp(2πi/3)\omega = \exp(2 \pi i / 3). Then draw an 11-sided polygon PP whose vertices are Eisenstein integers. Along each edge of PP, draw an equilateral triangle pointing inward. Make sure to choose the polygon PP so that these triangles touch each other only at its corners.

If you remove these triangles, you are left with an 11-pointed star. You can always fold up this star so all its tips meet at one point, creating a convex polyhedron. This in turn gives a triangulation of the 2-sphere, where the triangles are those coming from the lattice of Eisenstein integers. 5 or 6 triangles will meet at each vertex.

Thurston proved a remarkable fact: using this method, you can get all triangulations of the 2-sphere where 5 or 6 triangles meet at each vertex. (By Euler’s formula or the Gauss–Bonnet theorem, there will always be 12 vertices where 5 triangles.)

In the above example, which is the one featured in my AMS Notices column, Gerard Westendorp got a polyhedron called the hexagonal antiprism.

But in my column I posed the following puzzle: how can you get the regular icosahedron?

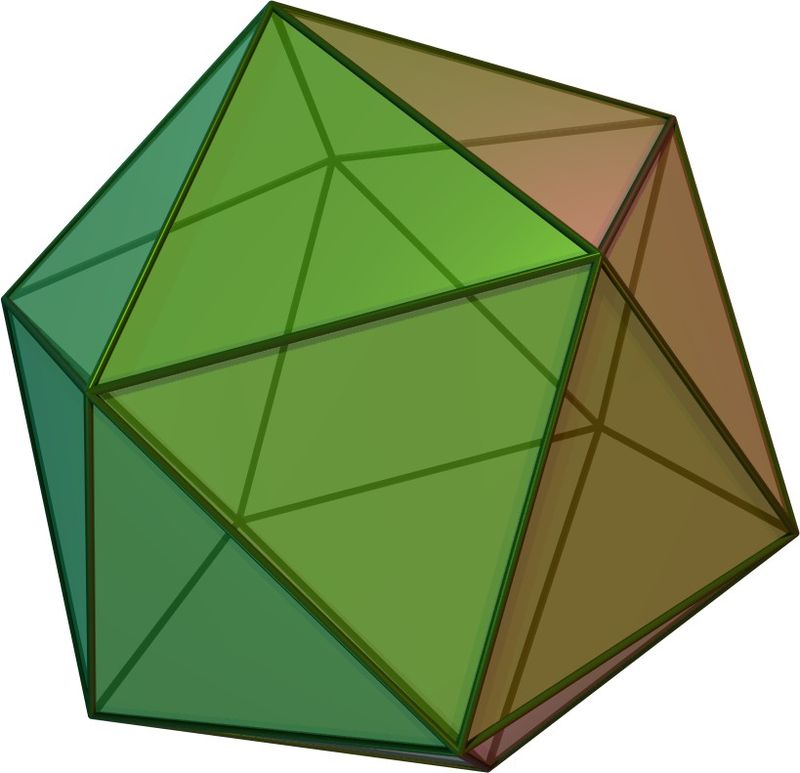
Here is Westendorp’s answer:

Want to check his work? Print it out, cut out the star, and fold it up!

Posted at November 5, 2024 11:18 PM UTC

TrackBack URL for this Entry:   https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/3577



4 Comments & 0 Trackbacks

Two different answers

The photo and the diagram do not match.

Posted by: Steve Huntsman on November 6, 2024 1:44 PM | Permalink | Reply to this

Re: Two different answers

The photo shows a hexagonal antiprism. The diagram in the photo has two red vertices (or rather, a red vertex and two red half-vertices) which are the centres of the two hexagonal faces of the diagram.

The diagram at the bottom of the post shows a regular icosahedron. To see why this is believable, observe that every interior vertex has an angle deficit of exactly 60°, and so by Gauss–Bonet this is also true for the exterior vertex (where all the peripheral vertices meet). This is not by itself a complete proof — you also have to convince yourself that the interior edges are all creased — but it helps make it believable, and perhaps it can be upgraded to a complete proof.

Posted by: Theo Johnson-Freyd on November 6, 2024 5:32 PM | Permalink | Reply to this

Re: Two different answers

Steve wrote:

The photo and the diagram do not match.

This is confusing to, since I showed a photo of a diagram, and separately a diagram of something completely different. The photo of the diagram matches the diagram it’s a photo of — I promise — while it’s not intended to match the diagram it’s not a photo of.

Posted by: John Baez on November 6, 2024 6:54 PM | Permalink | Reply to this

Re: The Icosahedron as a Thurston Polyhedron

Here’s a way to argue that Gerard’s solution to my puzzle is correct. Thurston showed that any star of the sort I described folds up so that all 11 of its tips touch and you get a convex polyhedron. Thus, this diagram must give some convex polyhedron:

and we just need to show it’s the regular icosahedron.

To do this, it’s enough to show it’s a polyhedron with equilateral triangular faces, with 12 vertices, and 5 triangles meeting at each vertex.

Here’s a rough argument, which would need to be improved to become a proof.

1) First let’s show that — like all Thurston polyhedra — this polyhedron has 12 points with 5 yellow triangles meeting at them.

That’s easy to see for the 11 vertices that arise from the 11 ‘indentations’ of the star. Each of those indentations arises from cutting out a green equilateral triangle, so when we fold up our star each indentation gives a vertex with an angle deficit of π/3. Thus, 5 small equilateral triangles must meet there: one short of the 6 you’d need to eliminate the angle deficit.

But what about the 12th vertex of our polyhedron, the one where all the tips of our star meet when we fold it up? Why do 5 small equilateral triangles meet there?

We could just look and think about it. But it’s easier to invoke Gauss–Bonnet (or Euler’s formula) which implies that the sum of the angle deficits at the vertices of a convex polyhedron is always 4π4 \pi. Since we’ve already seen 11 vertices of our polyhedron have an angle deficit of π/3\pi/3, the 12th must have an angle deficit of

4π−11⋅π3=12−113π=π3 4\pi - 11 \cdot \frac{\pi}{3} = \frac{12 - 11}{3} \pi = \frac{\pi}{3}

as well. So 5 small equilateral triangles must meet there too!

Then let’s note that in this polyhedron–unlike all the other Thurston polyhedra—there are no points at which 6 triangles meet. There are none visible from the start in our star, and none get formed when we fold it up. For comparison, in the example of the hexagonal antiprism, there is one such point visible from the start, and 1 more gets formed when we fold it up. Gerard has marked them both:

So, I argue, the polyhedron we get has only equilateral triangular faces, and 12 vertices at which 5 faces meet. Thus, by known facts, it’s the regular icosahedron.

(It’s fun to look for soft spots in this argument.)

Posted by: John Baez on November 7, 2024 12:45 AM | Permalink | Reply to this

Post a New Comment