Hyperbolic Kac–Moody Groups
Posted by John Baez
Just as the theory of finite-dimensional simple Lie algebras is connected to differential geometry and physics via the theory of simple Lie groups, the theory of affine Lie algebras is connected to differential geometry and physics by the realization that these are the Lie algebras of central extensions of loop groups:
Andrew Pressley and Graeme Segal, Loop Groups, Oxford U. Press, Oxford, 1988.
Graeme Segal, Loop groups.
Indeed it’s not much of an exaggeration to say that central extensions of loop groups are to strings as simple Lie groups are to particles!
What comes next?
The finite-dimensional simple Lie algebras and affine Lie algebras are both special class of Kac–Moody algebras. The natural next class is the hyperbolic Kac–Moody algebras.
Here are the Dynkin diagrams of the finite-dimensional simple Lie algebras:

Here are the Dynkin diagrams of the so-called ‘untwisted’ affine Lie algebras:

and the ‘twisted’ ones:
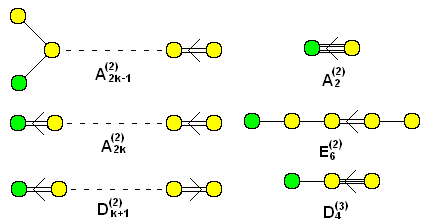
A Dynkin diagram describes a hyperbolic Kac–Moody algebra if it’s not any of those shown above, but every proper connected subdiagram is! There are infinitely many hyperbolic Kac–Moody algebras whose Dynkin diagrams have nodes, but only 238 with nodes. They’re listed here:
- Lisa Carbone, Sjuvon Chung, Leigh Cobbs, Robert McRae, Debajyoti Nandi, Yusra Naqvi and Diego Penta, Classification of hyperbolic Dynkin diagrams, root lengths and Weyl group orbits.
The ‘simply-laced’ ones were nicely drawn by Allcock and Carbone:
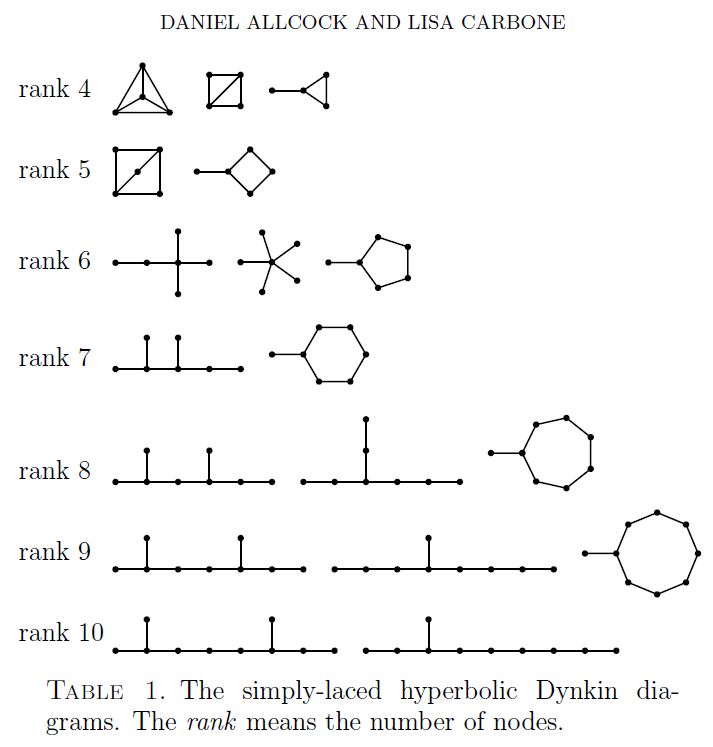
Concretely, the nodes in such a diagram stand for spacelike vectors in -dimensional Minkowski spacetime, where each vector has:
• inner product with itself,
• inner product with any vector corresponding to a node connected to it by an edge, and
• inner product with any vector corresponding to a node not connected to it by an edge.
These are the only ways to build such arrangements of vectors in the various dimensions listed! dimensions is the maximum possible. There must be a connection to string theory, but there’s also a direct explanation. Only in hyperbolic space of dimension can we find a simplex whose faces are either at ° or ° angles to each other!
The last and best of these diagrams is called . It’s connected to the octonions, it’s connected to -dimensional supergravity, and there are lots of interesting conjectures about its role in physics — see Allcock and Carbone’s paper for references, or this:
- John Baez, Integer octonions.
I’m wondering whether there is a geometrical construction of the groups corresponding to the hyperbolic Kac–Moody Lie algebras. Since after ‘particle’ and ‘string’ one naturally says ‘2-brane’, one might naively hope that this geometrical construction would be connected to 2-brane theories, or 2+1-dimensional field theories. But maybe that’s the wrong idea.
Jacques Tits found a way to construct Kac–Moody groups, not only over the real and complex numbers but over arbitrary commutative rings:
- Jacques Tits, Uniqueness and presentation of Kac–Moody groups over fields, Journal of Algebra 105 (1987), 542–573.
This has been simplified for a certain class of hyperbolic Kac–Moody groups, namely the simply-laced ones:
- Daniel Allcock, Lisa Carbone, Presentation of hyperbolic Kac–Moody groups over rings.
But this construction does not feel ‘geometric’ to me: it’s in terms of generators and relations.


Re: Hyperbolic Kac–Moody Groups
Thank you for highlighting my work with Lisa! Indeed the main frustration of the theory is that it is so far not very geometric. is lovely but the Kac–Moody groups should be as geometric as Lie groups, and they are not, yet.
It may interest some people that the simplification in Tits’ description of the groups over rings holds in greater generality than those specific hyperbolic diagrams. The same presentation works for any simply laced Dynkin diagram. If you allow multiple bonds then you have to assume that that the ground ring has no tiny fields as quotients ( if there is a double bond, or if there is a triple bond), or that the Dynkin diagram is “3-spherical”, meaning that the any 3-node subdiagram comes from a finite-dimensional Lie algebra. See arXiv:1307.2689. The hypotheses on the ring can be omitted for affine diagrams (arXiv:1409.0176, to appear in Algebra and Number Theory).