The n-Category Café

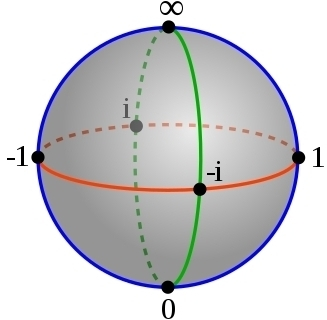
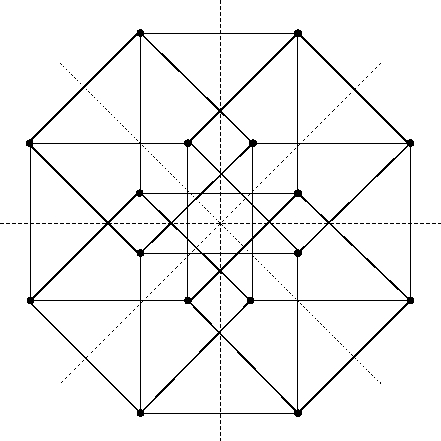
The complex numbers together with infinity form a sphere called the Riemann sphere. The 6 simplest numbers on this sphere lie at points we could call the north pole, the south pole, the east pole, the west pole, the front pole and the back pole. They’re the corners of an octahedron!

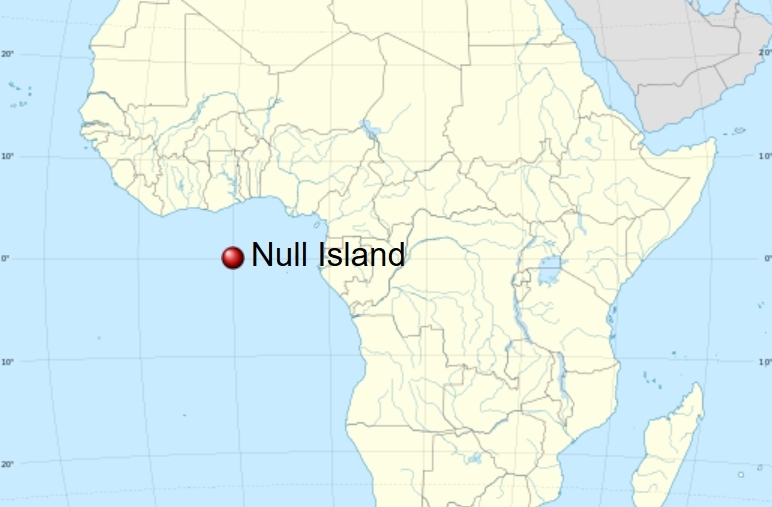
On the Earth, we all know where the north pole and south pole are. I’d say the “front pole” is where the prime meridian meets the equator at 0°N 0°E. It’s called Null Island, but there’s no island there—just a buoy. Here it is:

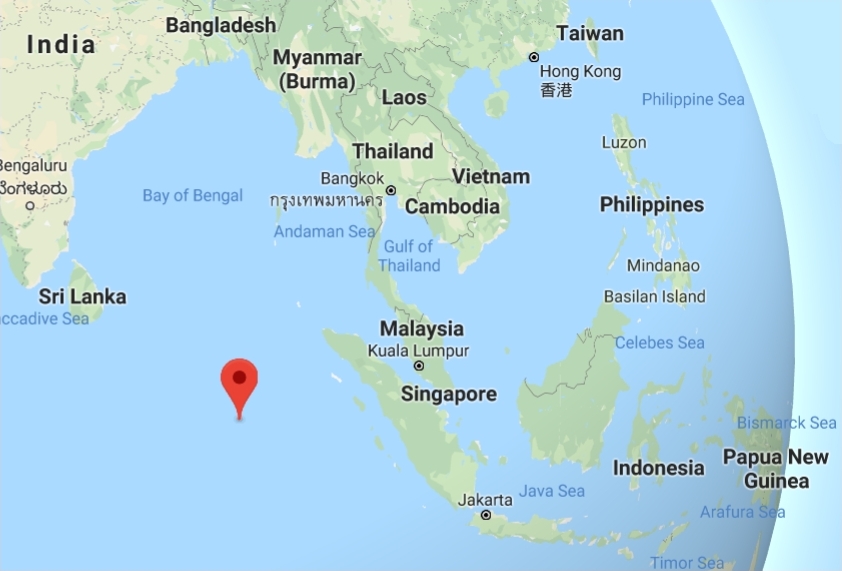
Where’s the back pole, the east pole and the west pole? I’ll leave two of these as puzzles, but I discovered that in Singapore I’m fairly close to the east pole:

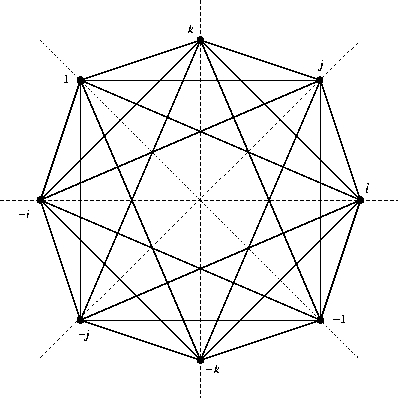
If you think of the octahedron’s corners as the quaternions $\pm i, \pm j, \pm k,$ you can look for unit quaternions $q$ such that whenever $x$ is one of these corners, so is $q x q^{-1}$. There are 48 of these! They form a group called the binary octahedral group.

By how we set it up, the binary octahedral group acts as rotational symmetries of the octahedron: any transformation sending $x$ to $q x q^{-1}$ is a rotation. But this group is a double cover of the octahedron’s rotational symmetry group! That is, pairs of elements of the binary octahedral group describe the same rotation of the octahedron.

If we go back and think of the Earth’s 6 poles as points $0, \pm 1,\pm i, \infty$ on the Riemann sphere instead of $\pm i, \pm j, \pm k$, we can think of the binary octahedral group as a subgroup of $\mathrm{SL}(2,\mathbb{C}$), since this acts as conformal transformations of the Riemann sphere!

If we do this, the binary octahedral group is actually a subgroup of $\mathrm{SU}(2)$, the double cover of the rotation group—which is isomorphic to the group of unit quaternions. So it all hangs together.

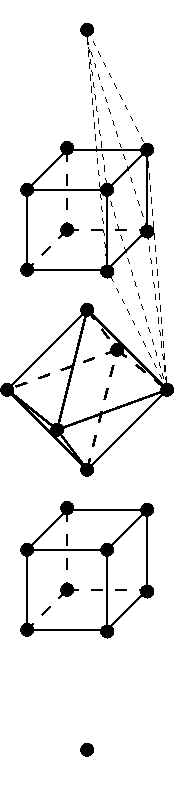
It’s fun to actualy see the unit quaternions in the binary octahedral group. First we have 8 that form a group on their own, called the quaternion group:

$$\pm 1, \pm i , \pm j , \pm k$$

These are the vertices of the 4d analogue of an octahedron, called a cross-polytope. It looks like this:

Then we have 16 that form the corners of a hypercube (the 4d analogue of a cube, also called a tesseract or 4-cube):

$$\displaystyle{ \frac{\pm 1 \pm i \pm j \pm k}{2} }$$

They look like this:

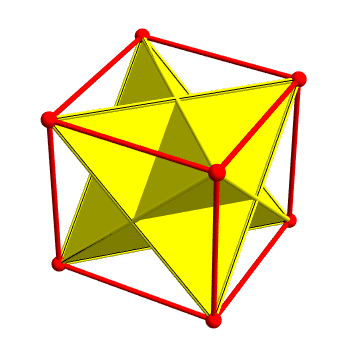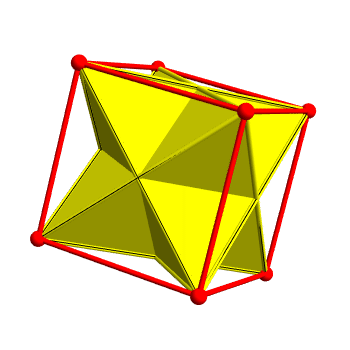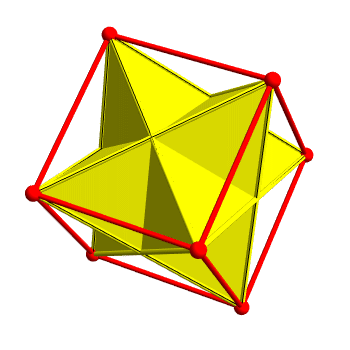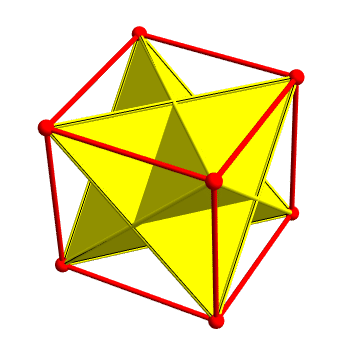
These don’t form a group, but if we take them together with the 8 previous ones we get a 24-element subgroup of the unit quaternions called the binary tetrahedral group. These 24 elements are also the vertices of the 24-cell, which is the one regular polytope in 4 dimensions that doesn’t have a 3d analogue. It looks like this:

This shape is called the 24-cell not because it has 24 vertices, but because it also has 24 faces, which happen to be regular octahedra. You can see one if you slice the 24-cell like this:

The slices here have real part 1, ½, 0, -½, and -1 respectively. Note that the slices with real part ±½ contain the vertices of a hypercube, while the rest contain the vertices of a cross-polytope.

And here’s another great way to think way about binary tetrahedral group. We’ve seen that if you take every other vertex of a cube you get the vertices of a regular tetrahedron. Similarly, if you take every other vertex of a 4d hypercube you get a 4d cross-polytope. So, you can take the vertices of a 4d hypercube and partition them into the vertices of two cross-polytopes. As a result, the 24 elements of the binary tetrahedral group can be partitioned into three cross-polytopes! Greg Egan shows how it looks:

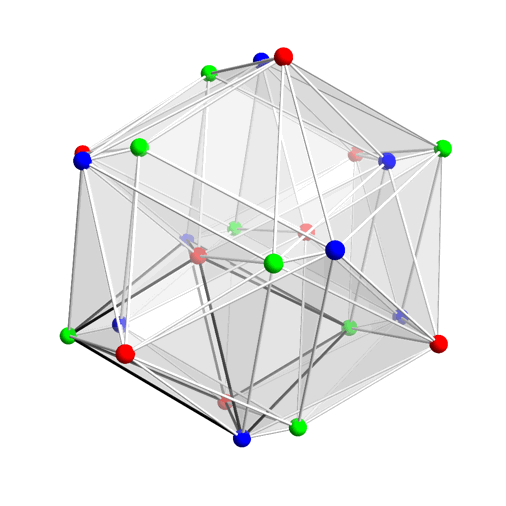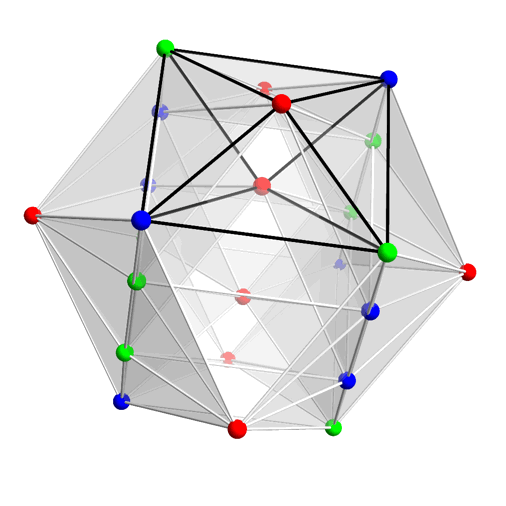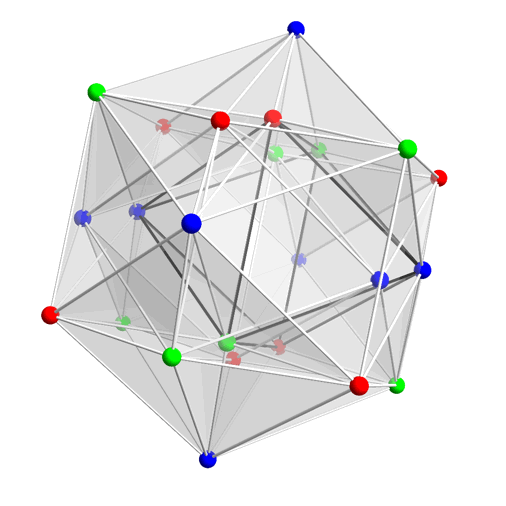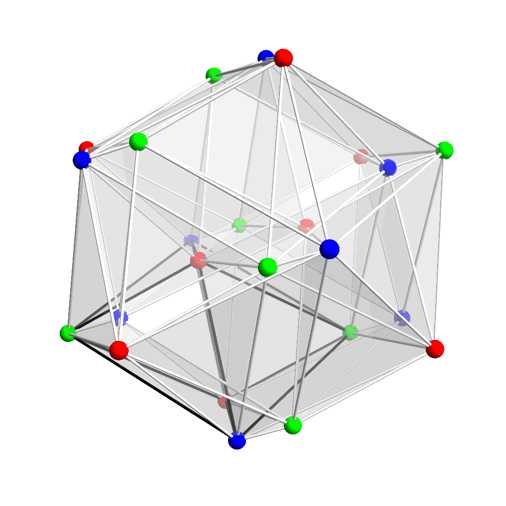
So far we’ve accounted for half the quaternions in the binary octahedral group! Here are the other 24:

$$\displaystyle{ \frac{\pm 1 \pm i}{\sqrt{2}}, \frac{\pm 1 \pm j}{\sqrt{2}}, \frac{\pm 1 \pm k}{\sqrt{2}}, }$$

$$\displaystyle{ \frac{\pm i \pm j}{\sqrt{2}}, \frac{\pm j \pm k}{\sqrt{2}}, \frac{\pm k \pm i}{\sqrt{2}} }$$

These form the vertices of another 24-cell! So the binary octahedral group can be built by taking the vertices of two separate 24-cells. And in fact, these two 24-cells are ‘dual’ to each other: the vertices of each one hover right above the centers of the faces of the other!

The first 24 quaternions, those in the binary tetrahedral group, give rotations that preserve each one of the two tetrahedra that you can fit around an octahedron—or in a cube:

while the second 24 switch these tetrahedra.

Greg has nicely animated the 48 elements of the binary octahedral group here:

He’s colored them according to the rotations of the octahedron they represent. Remember: in the binary octahedral group, two elements $q$ and $-q$ describe each rotational symmetry of the octahedron. And here they are:

Black: the 2 elements

$$\pm 1$$

act as the identity.

Blue: the 12 elements

$$\displaystyle{ \frac{\pm 1 \pm i}{\sqrt{2}}, \frac{\pm 1 \pm j}{\sqrt{2}}, \frac{\pm 1 \pm k}{\sqrt{2}} }$$

describe ±90° rotations around the octahedron’s 3 axes.

Red: the 16 elements

$$\displaystyle{ \frac{\pm 1 \pm i \pm j \pm k}{2} }$$

describe 120° rotations of the octahedron’s 8 triangles.

Yellow: The 6 elements

$$\pm i , \pm j , \pm k$$

describe 180° rotations around the octahedron’s 3 axes.

Cyan: the 12 elements

$$\displaystyle{ \frac{\pm i \pm j}{\sqrt{2}}, \frac{\pm j \pm k}{\sqrt{2}}, \frac{\pm k \pm i}{\sqrt{2}} }$$

describe 180° rotations of the octahedron’s 6 opposite pairs of edges.

Finally, here’s another fun fact about the binary octahedral group that follows from what we’ve already seen. Note that because

• we can partition the 48 vertices of the binary octahedral group into two 24-cells

and

• we can partition the 24 vertices of the 24-cell into three cross-polytopes

it follows that we can partition the 48 vertices of the binary octahedral group into six cross-polytopes!

I don’t know the deep meaning of this fact. I know that the vertices of the 24-cell correspond to the 24 roots of the Lie algebra $\mathfrak{so}(8).$ I know that the the famous ‘triality’ symmetry of $\mathfrak{so}(8)$ permutes the three cross-polytopes in the 24-cell, which are in some rather sneaky way related to the three 8-dimensional irreducible representations of $\mathfrak{so}(8).$ I also know that if we take the two 24-cells in the binary octahedral group, and expand one by a factor of $\sqrt{2},$ so the vertices of other lie exactly at the center of its faces, we get the 48 roots of the Lie algebra $\mathfrak{f}_4.$ But I don’t know how to extend this story to get a nice story about the six cross-polytopes in the binary octahedral group.

All I know is that if you pick a quaternion group sitting in the binary octahedral group, it will have 6 cosets, and these will be six cross-polytopes.