Skip to the Main Content

Note:These pages make extensive use of the latest XHTML and CSS Standards. They ought to look great in any standards-compliant modern browser. Unfortunately, they will probably look horrible in older browsers, like Netscape 4.x and IE 4.x. Moreover, many posts use MathML, which is, currently only supported in Mozilla. My best suggestion (and you will thank me when surfing an ever-increasing number of sites on the web which have been crafted to use the new standards) is to upgrade to the latest version of your browser. If that's not possible, consider moving to the Standards-compliant and open-source Mozilla browser.

August 15, 2023

8 and 24

Posted by John Baez

On 8/24 I’m giving a talk about the numbers 8 and 24.

Abstract. The numbers 8 and 24 play special roles in mathematics. The number 8 is special because of Bott periodicity, the octonions and the E8 lattice, while 24 is special for many reasons, including the binary tetrahedral group, the 3rd stable homotopy group of spheres, and the Leech lattice. The number 8 does for superstring theory what the number 24 does for bosonic string theory. In this talk, which is intended to be entertaining, I will overview these matters and also some connections between the numbers 8 and 24.

You can see slides and a video of my talk here.

Juven Wang had the hilarious idea of scheduling this talk on 8/24 for his Quantum Matter in Mathematics and Physics seminar at Harvard. So while it’s intended to be entertaining, it’s mainly aimed at entertaining folks who know a fair amount of math and physics. If you want a less stressful version, try these videos instead:

A bunch of middle school students liked the first one!

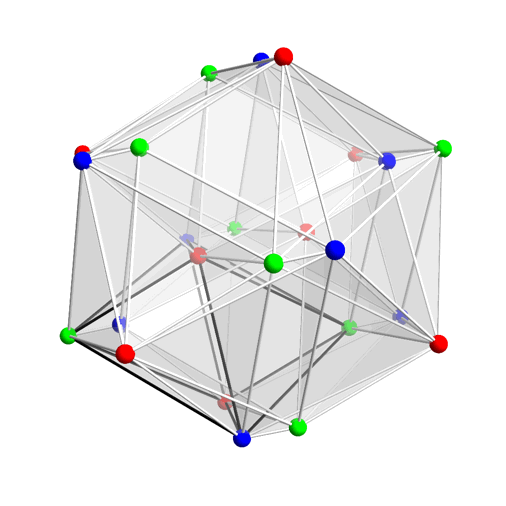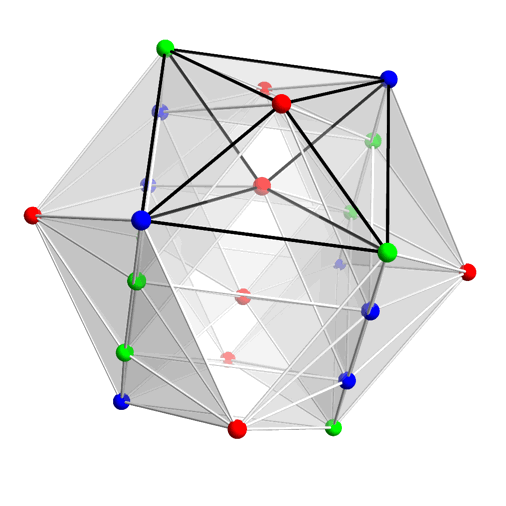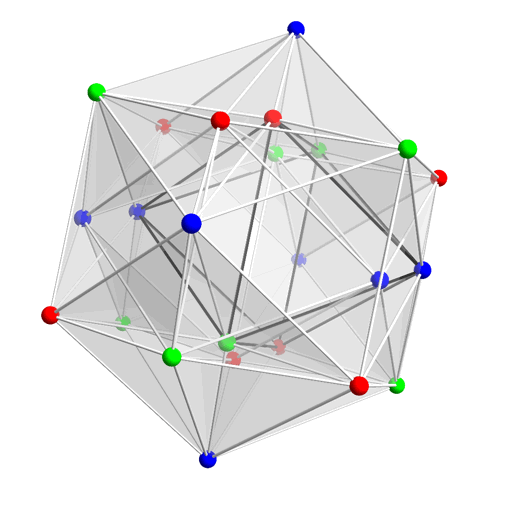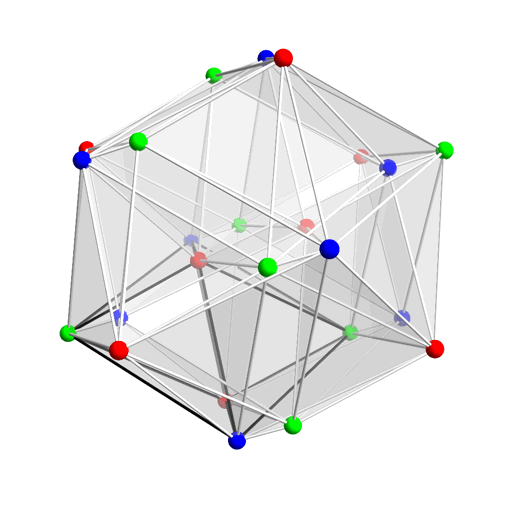
If you want to understand how this gif by Greg Egan connects the numbers 8 and 24, click on it. Briefly, it shows the 24-cell, a Platonic solid in 4 dimensions. Its 24 vertices are grouped into three bunches of 8, colored red green and blue. These correspond to the three 8-dimensional representations of double cover of the rotation group in 8 dimensions: the vector rep, the left-handed spinor rep, and the right-handed spinor rep. Operators involving these three 8-dimensional spaces give rise to the octonions!

Posted at August 15, 2023 8:36 AM UTC

TrackBack URL for this Entry:   https://golem.ph.utexas.edu/cgi-bin/MT-3.0/dxy-tb.fcgi/3485



5 Comments & 0 Trackbacks

Thomas

The link to the YouTube playlist is wrong; it should go to https://www.youtube.com/playlist?list=PLuAO-1XXEh0ZiJlRKz7EuODAdIOjC5-1l

Posted by: Thomas Colthurst on August 24, 2023 7:37 PM | Permalink | Reply to this

Re: Thomas

I was trying to link to the Quantum Matter Seminar playlist but screwed up; you’ve given the link to my playlist, which works now that I’ve added the video there — but this webpage is even better since there the video automatically starts at 3:55, which is when my talk starts — and you can see my slides there too.

Posted by: John Baez on August 24, 2023 9:16 PM | Permalink | Reply to this

Re: 8 and 24

I think the talk went well! Maybe it will attract the attention of the person to make the next big breakthrough in 24-ology.

Posted by: Blake Stacey on August 24, 2023 9:45 PM | Permalink | Reply to this

Re: 8 and 24

Thanks! Maybe they can leap from the rotating tetrahedron to the superstring and bosonic string in a single bound.

Posted by: John Baez on August 25, 2023 10:08 AM | Permalink | Reply to this

Re: 8 and 24

I was sure that this post was going to be about this result, which features 8 and 24: https://www.quantamagazine.org/two-students-unravel-a-widely-believed-math-conjecture-20230810/

Within half a day, Rickards came around. The pattern ruled out all pairs where the first number is of the form 8 × (3n ± 1)2 and the second is 24 times any square. This means 24 and 8 never appear in the same packing. Numbers you’d expect to occur don’t.

Posted by: Joshua Holden on August 26, 2023 9:43 PM | Permalink | Reply to this

Post a New Comment