Skew-Monoidal Categories: Logical and Graphical Calculi
Posted by Emily Riehl
guest post by Wilf Offord
One of the earliest and most well-studied definitions in “higher” category theory is that of a monoidal category. These have found ubiquitous applications in pure mathematics, physics, and computer science; from type theory to topological quantum field theory. The machine making them tick is MacLane’s coherence theorem: if anything deserves to be called “the fundamental theorem” of monoidal categories, it is this. As such, numerous other proofs have sprung up in recent years, complementing MacLane’s original one. One strategy with a particularly operational flavour uses rewriting systems: the morphisms of a free monoidal category are identified with normal forms for some rewriting system, which can take the form of a logical system as in (UVZ20,Oli23), or a diagrammatic calculus as in (WGZ22). In this post, we turn to skew-monoidal categories, which no longer satisfy a coherence theorem, but nonetheless can be better understood using rewriting methods.
Monoidal Categories
Monoidal categories are categories equipped with a “product” of objects, which is associative and unital “up to isomorphism” in a specified sense. An example is the category of sets with its cartesian product: while the sets and are not technically equal, they are isomorphic, via an isomorphism which is in some sense canonical. More precisely:
Definition: A monoidal category consists of the following data:
- A category
- A functor
- An object
- Isomorphisms natural in
- Isomorphisms and natural in
such that the following diagrams commute:
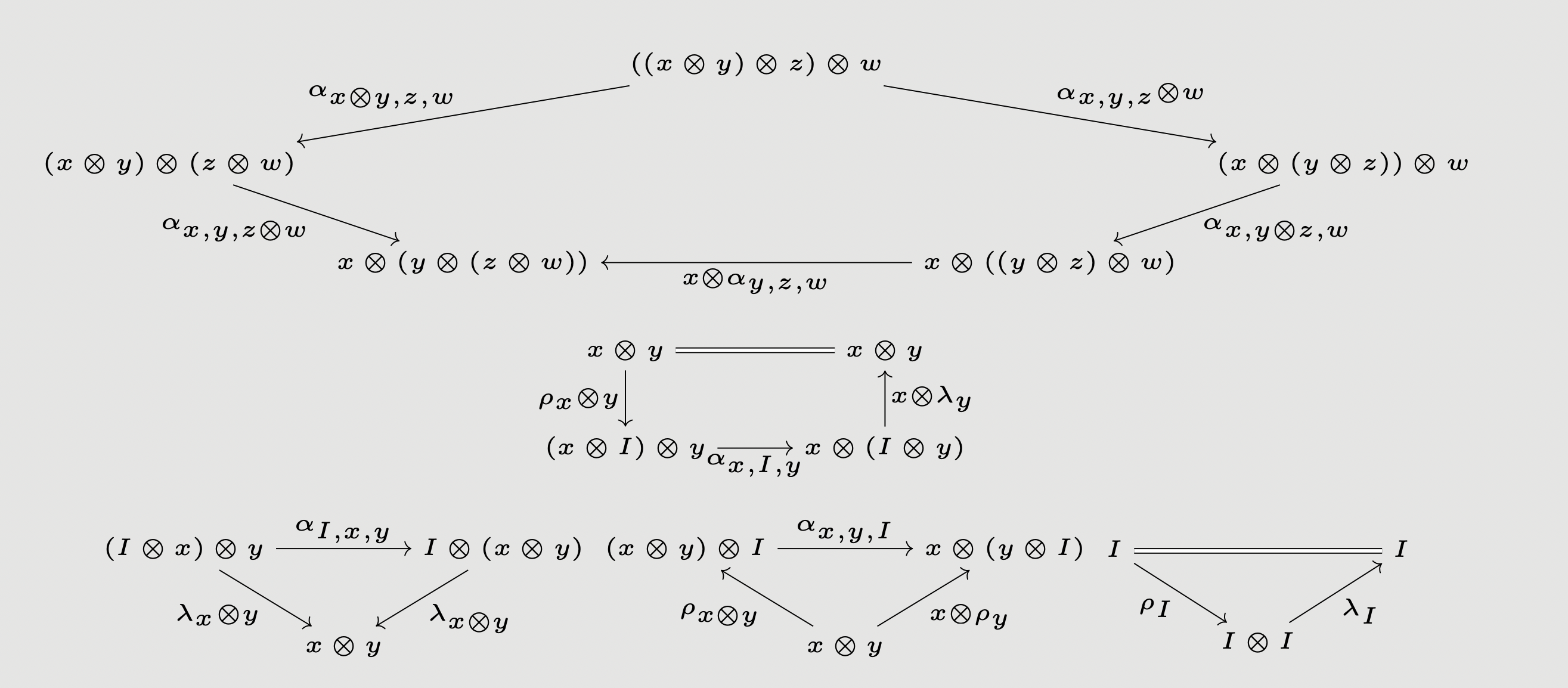
(for and , we write to mean , and similarly for )
Remark: The above is MacLane’s original definition of a monoidal category. It was later shown that the last three equations follow from the first two, but we include them since this does not hold for skew-monoidal categories, as we will present below.
The coherence theorem for monoidal categories can be stated in terms of the free monoidal category on a set of objects. We will not go into the formal definition, but this is the category whose objects are “formal products” of the elements of (e.g. , , etc.), and whose morphisms are only those built from , , , , and subject to the equations above and no other “accidental” equations. The coherence theorem is then:
Theorem: (MacLane’s coherence theorem) The free monoidal category on a set of objects is a preorder. That is, any two morphisms built from , , , , and between the same two objects are equal.
The above theorem is incredibly powerful, and implies that the equations listed above are strong enough to imply any other well-typed equation we could dream up in the language of monoidal categories. It was first proved in (Mac63), but we will investigate a few modern proof strategies later on in this post. First, though, we turn to skew-monoidal categories.
Skew-monoidal Categories
The above definition reflects a general pattern in higher category theory: equalities get replaced by isomorphisms. Let us explain what we mean by this. In a monoid, there is a product operation that is associative and unital on the nose, but when we “categorify” this definition, these associativity and unitality laws are promoted to pieces of the structure in their own right: the associator and unitor isomorphisms. This opens up an interesting direction for generalisation: what happens if we do not require the maps , , and to be invertible? The definition given above is phrased so as to still make sense once we drop the invertibility constraint, and doing so we obtain the definition of skew-monoidal categories.
Clearly every monoidal category is a skew-monoidal category, but we can also give some examples illustrating the new freedom that dropping the invertibility restraint allows.
Example: (Pointed Sets) Consider the category of sets with a chosen base point. Setting , and , there is an obvious choice for , , and (exercise: find these!) defining a skew-monoidal structure. Note the asymmetry in the definition of : due to this, is not injective and is not surjective! However, in this case we nevertheless have that is invertible.
Example: () We can put a skew-monoidal structure on , considered as a category whose objects are non-negative integers, and where there is exactly one morphism if . In fact, there are countably many such structures, one for each . We define:
- , where .
, , and are now the assertions that, for any :
- (so is invertible)
- ( is not in general invertible)
The next example requires a bit of background knowledge on Kan extensions, and can be skipped.
Example: Let be a functor, where is small and is cocomplete, so that all left Kan extensions of functors along exist. We can put a skew-monoidal structure on the functor category , where . The monoidal unit is . The universal property of left Kan extensions ensures we have natural morphisms:
If is fully faithful, then is an isomorphism. If is dense, meaning , then is an isomorphism. If is absolute for all , meaning the Kan extension is preserved by all functors, then is an isomorphism, and so in the case where all three of these properties hold, the above gives an ordinary monoidal category. However, we see that the most general case of this construction, involving only Kan extensions which are ubiquitous in category theory, naturally gives us not a monoidal category but a skew-monoidal one.
While the definitions of monoidal and skew-monoidal categories are not so different, they behave in very different ways. The most obvious question we can ask about skew-monoidal categories is whether a theorem like the coherence theorem holds. The answer turns out to be “no”: for instance, in the free skew-monoidal category generated by just the object , the morphisms and are not equal! If we want to understand the coherence morphisms of skew-monoidal categories, we will need a more nuanced approach.
Some modern approaches to the proof of the coherence theorem characterise coherences in monoidal categories as normal forms of some rewriting system; by showing that there is exactly one normal form of each given type, the coherence theorem is proved. But this approach can also be used to study skew-monoidal categories: while the example above shows we have no hope of having unique normal forms of each type, we can still get a much better picture of the structure by implementing it as a rewriting system. It is to these rewriting systems that we now turn.
Multicategories and Graphical Calculus
The rewriting systems we describe are all based on (skew) multicategories, which we will briefly introduce. The motivating idea is that while the morphisms of categories have one input and one output, the morphisms of multicategories have multiple inputs and one output. More precisely:
Definition: A multicategory consists of:
- A class of objects.
- For each pair of a (possibly empty) list of objects and an object , a class of multimorphisms from to .
- For each object , an element .
- Operations
is to be thought of as precomposition on the th input. These data are subject to equations that are analogues of associativity and unitality for ordinary categories, but these are best described using the graphical calculus for multicategories, which we now introduce.
Our graphical calculus is to be read top-to-bottom, and so we draw a multimorphism from to as:
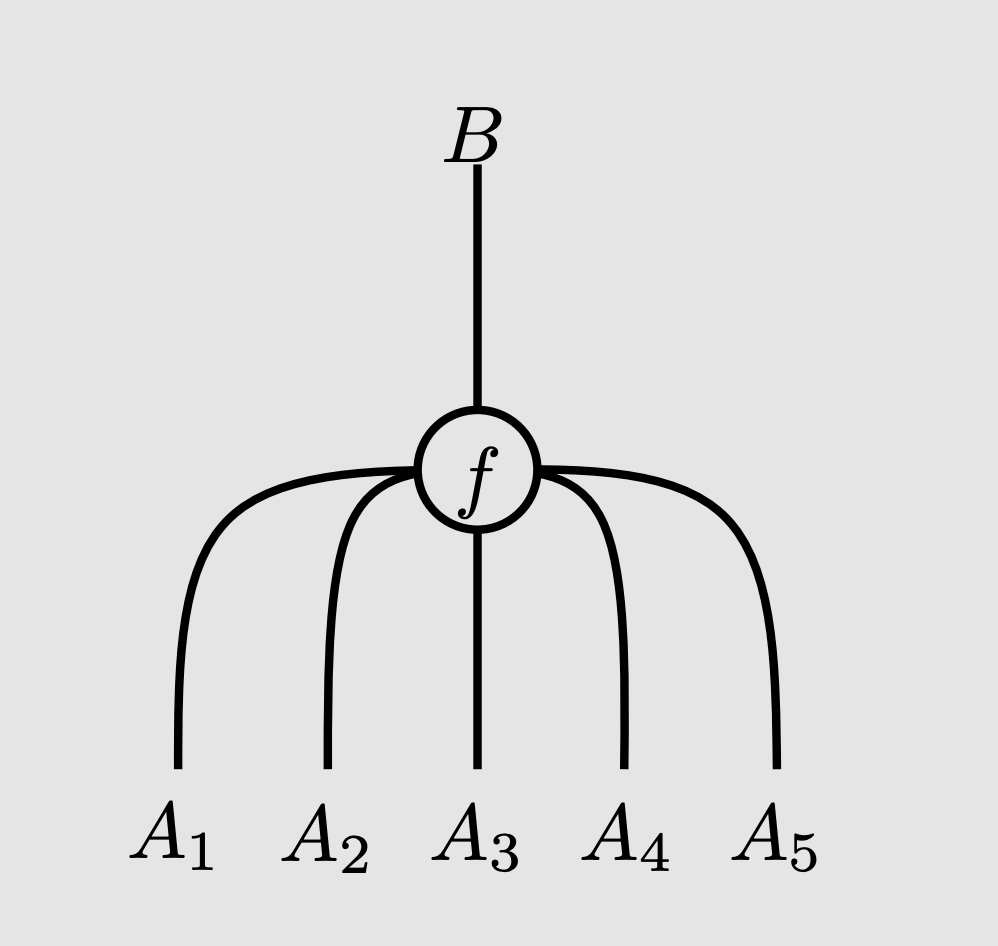
Identity morphisms are not drawn; the following represents :
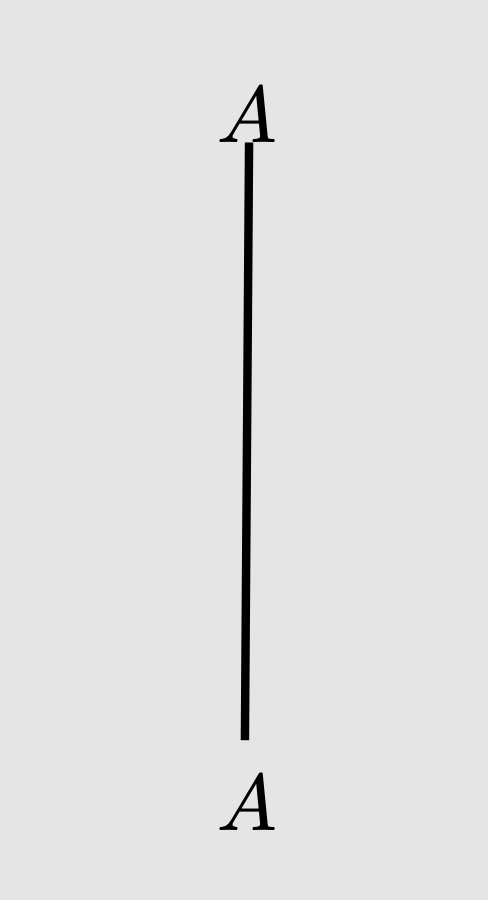
We denote the composite by:
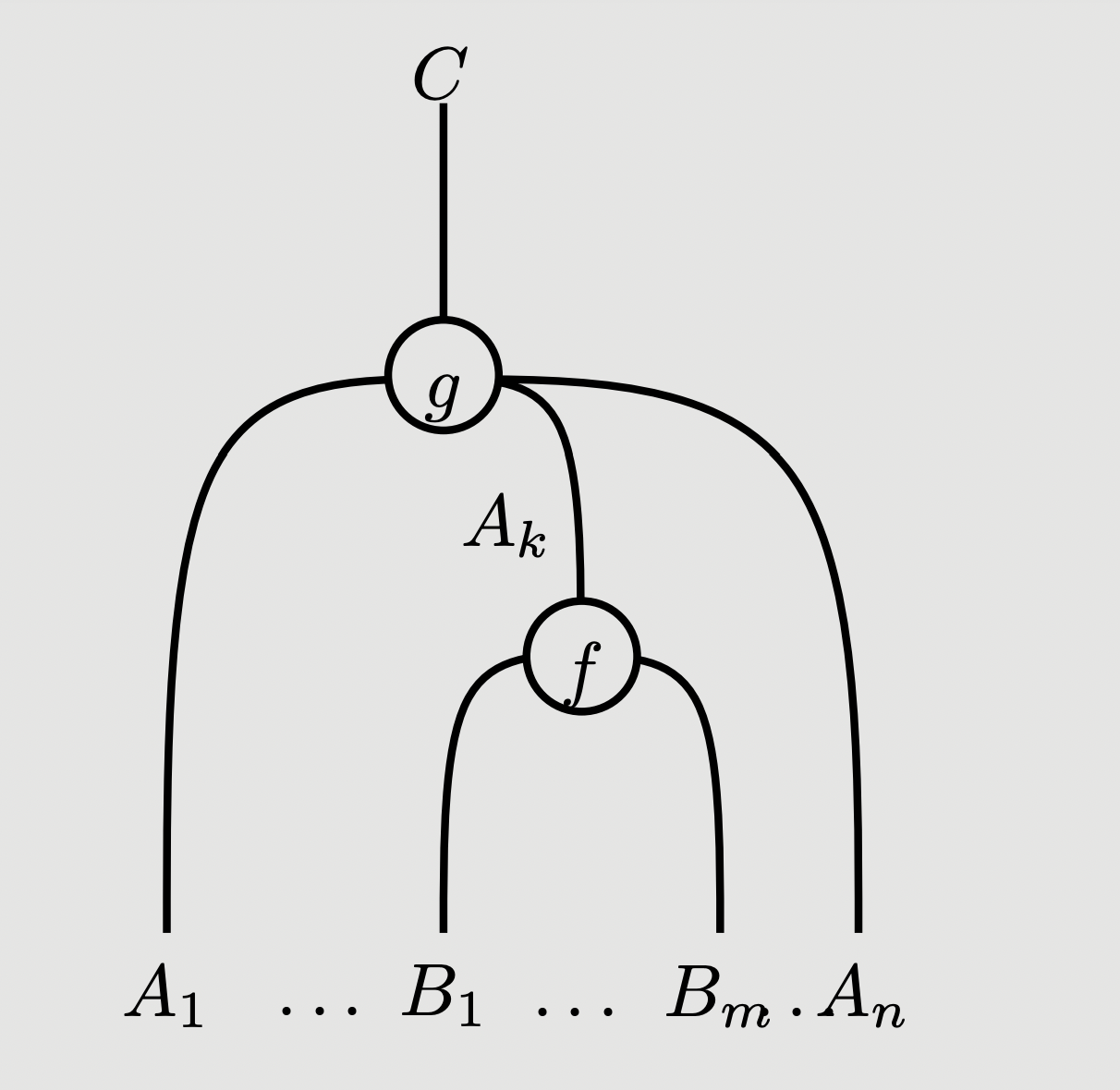
The unitality and associativity laws are then immediate from the graphical calculus, for instance is an equation that holds in the theory of multicategories for , , , and this equation holds in the graphical calculus up to planar isotopy of diagrams (or, less formally, “wiggling things around”):
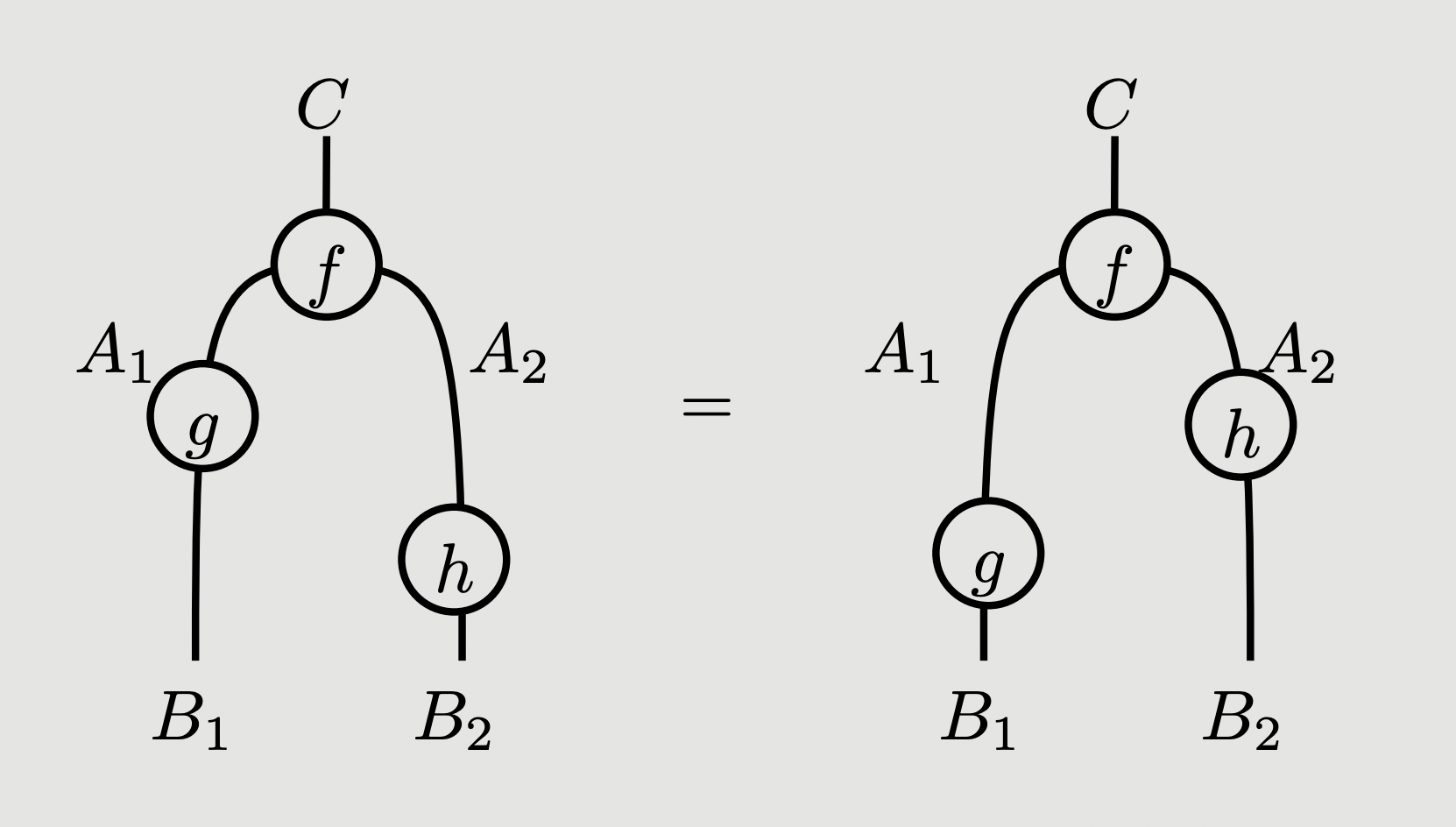
The reason for introducing multicategories is that they are intimately linked to monoidal categories. Given the structure of a monoidal category, the idea of “multiple inputs” can be encoded using the monoidal product, for instance . Indeed, every monoidal category can be given the structure of a multicategory . The difference between the two notions is that not all multicategories arise this way. Not all are “representable”, in the sense that there is a single object which encodes all the information about multimorphisms out of . To this end, we define:
Definition: A representable multicategory is a multicategory equipped with, for each list of objects of :
- An object . (When is empty, we denote this by )
- A multimorphism .
Such that is always an isomorphism.
The above definition is justified by the following:
Theorem: A multicategory is isomorphic to for some monoidal category if and only if it is representable.
(we have not technically defined isomorphism of multicategories: for details see Chapter 2 of (Lei03)). The above theorem, together with the fact that monoidal categories are isomorphic iff the corresponding multicategories are, imply a correspondence between representable multicategories and monoidal categories.
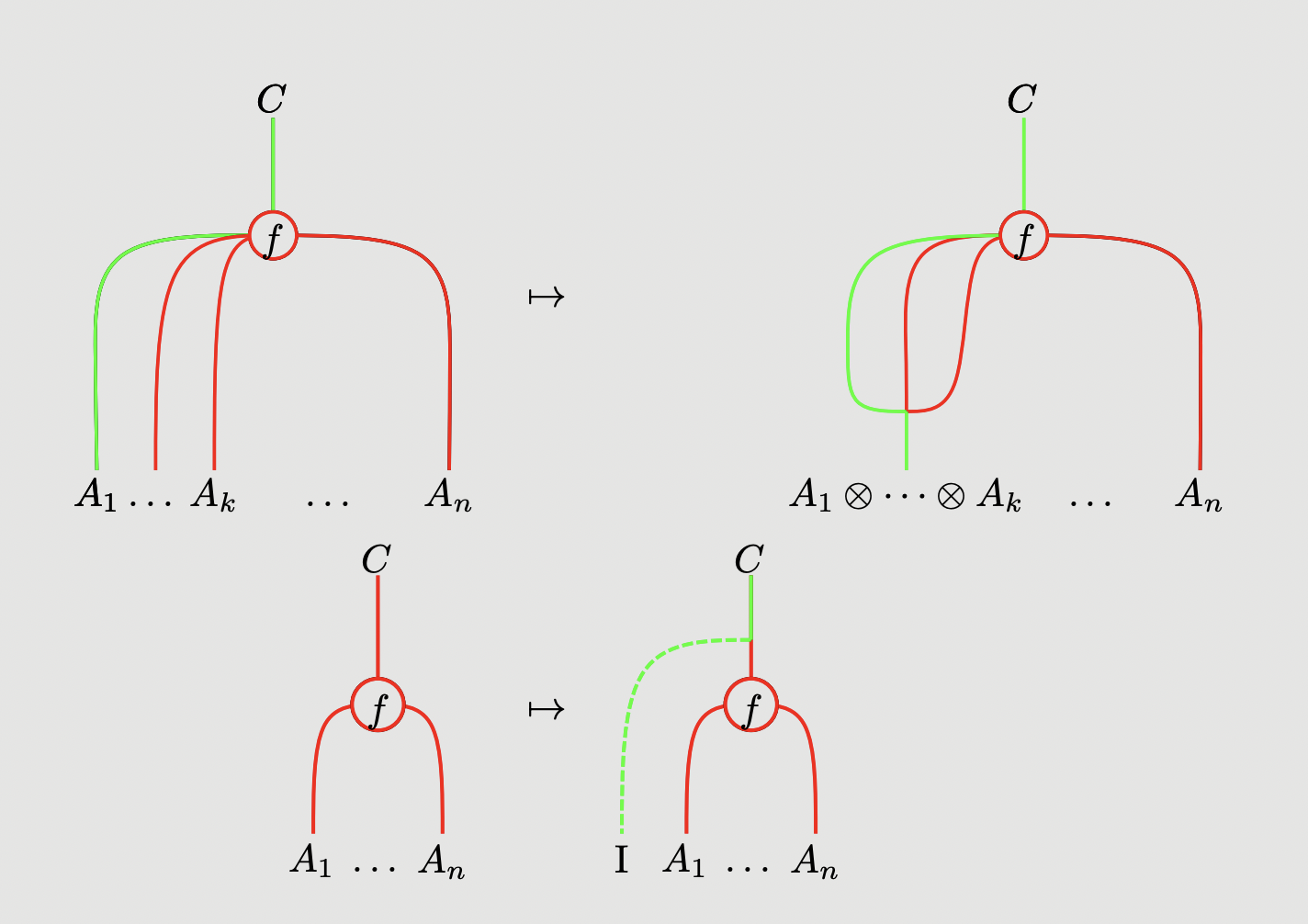
Given the additional structure of representability, we can add more power to our graphical calculus. We draw as:
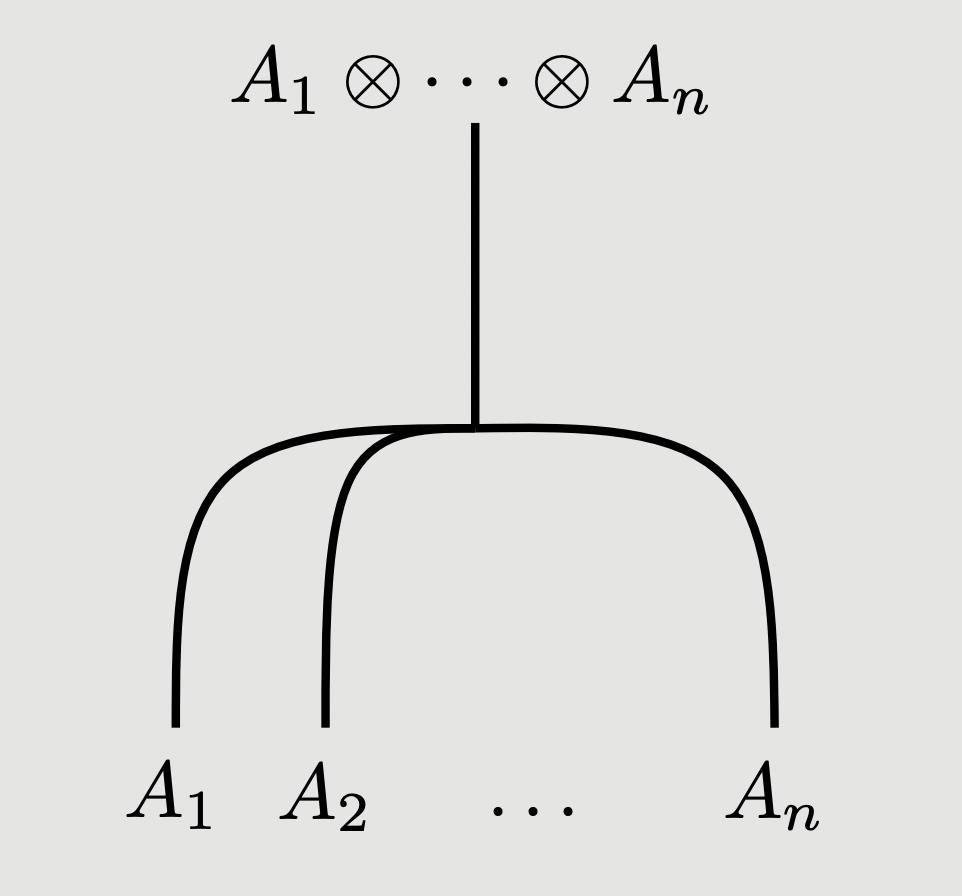
To express that is invertible, we represent the inverse, a map as:
In the case where is empty, we write the above as:
The above is subject to the equations expressing invertibility:
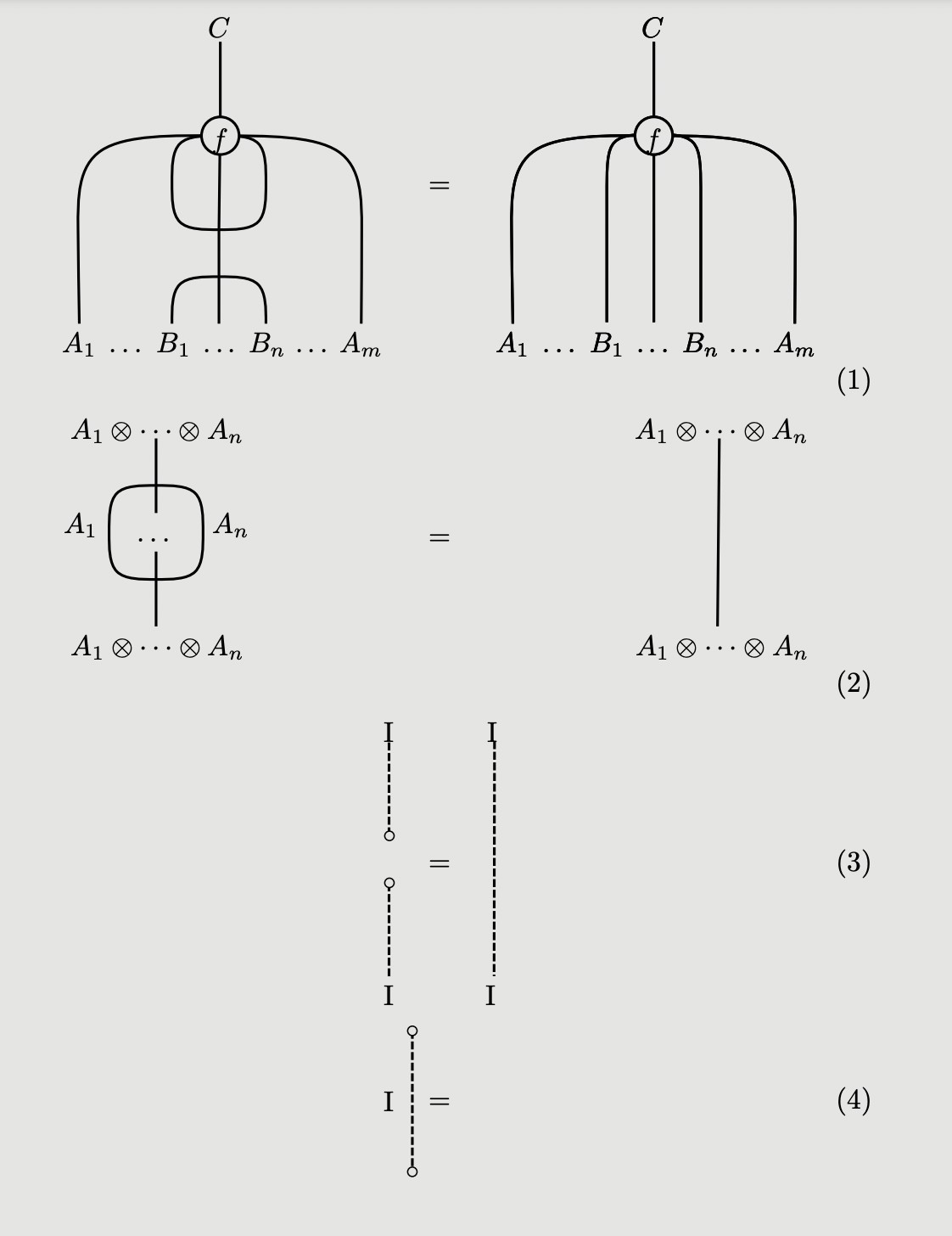
We now have a diagrammatic equational theory for represntable multicategories, and hence monoidal categories. Thus, all the coherences of a monoidal category should be expressible diagrammatically, along with the equations between them. For instance, the following represent the associator, left and right unitors:
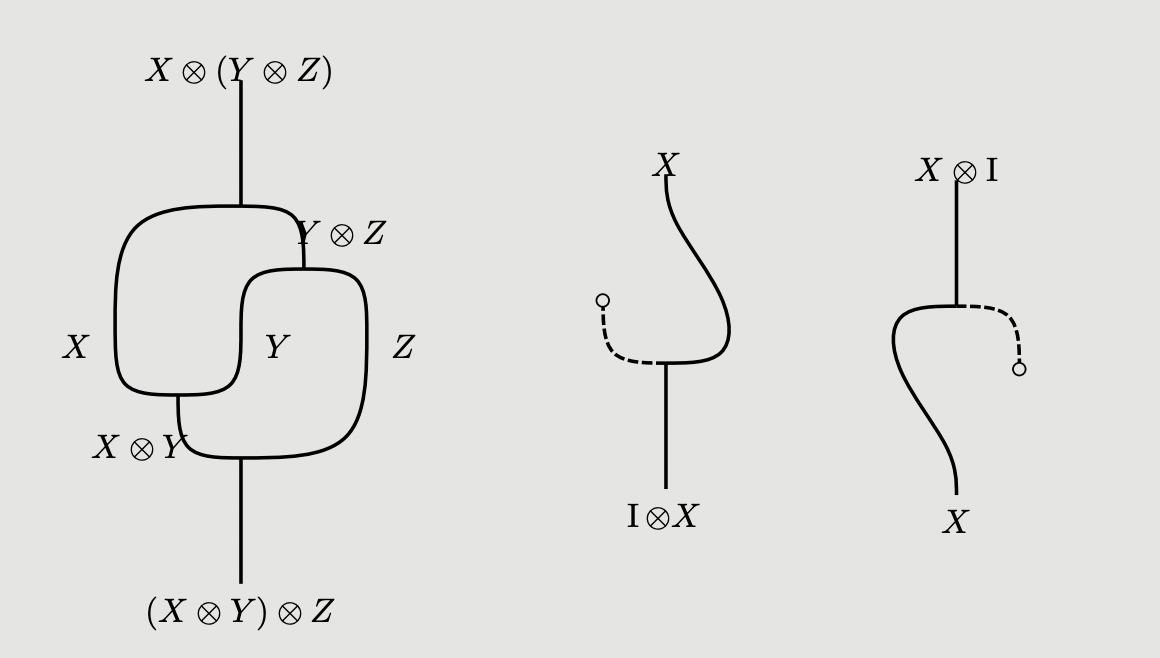
And their inverses as the vertically reflected versions:
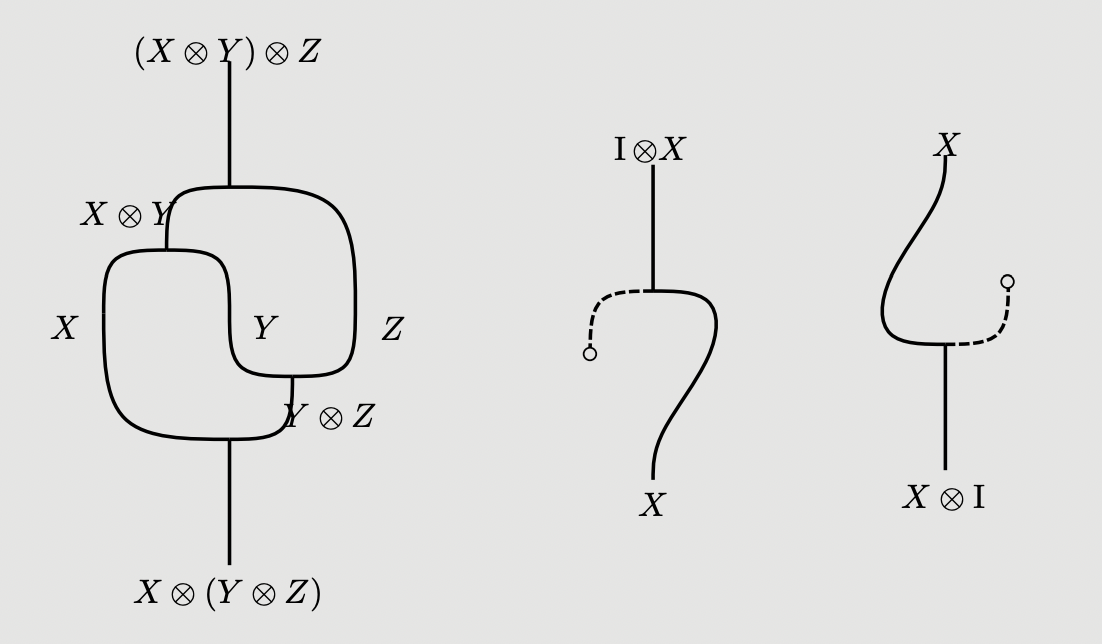
And the following is a derivation of , for instance:
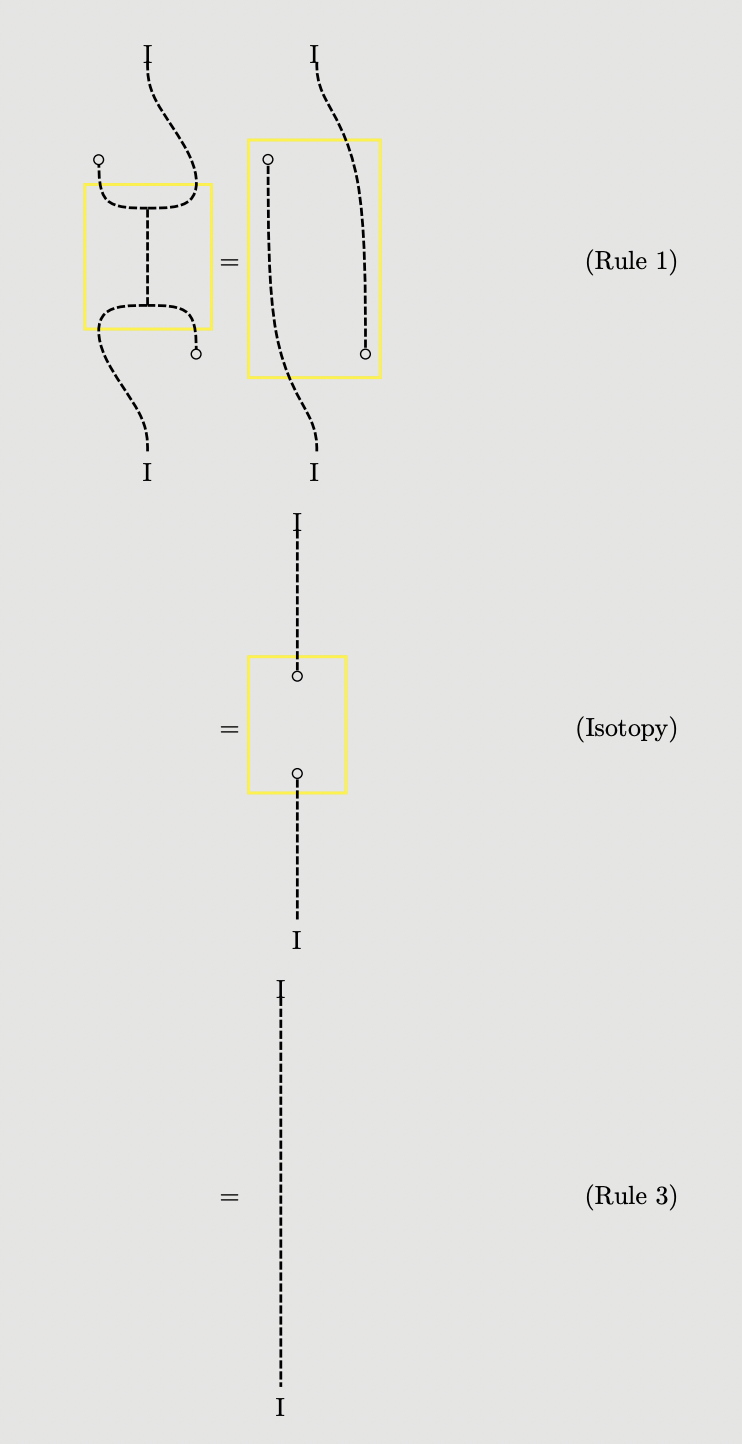
In fact, the above graphical calculus is exactly the same as that described in (WGZ22), although the way the authors arrive at it is completely different, having nothing to do with multicategories. Instead, they consider the strictification of a monoidal category. Moreover, they show using graphical methods that every diagram of the same type is equal, proving theorem the coherence theorem.
The strictification theorem for monoidal categories doesn’t have an analogue for skew-monoidal categories, and so the approach taken in (WGZ22) is not suitable to be adapted to this case. However, there is an analogue of multicategories, skew multicategories, defined in (BL18), to which we now turn.
Skew Multicategories
The idea of skew multicategories is that there are two kinds of multimorphisms, “tight” and “loose”, which behave differently with respect to composition. Loose morphisms behave like ordinary multimorphisms in a multicategory. Tight morphisms, on the other hand, can only be composed together on the leftmost input, via , and this is what leads to the asymmetry.
Definition: A skew multicategory consists of:
- A class of objects.
- For each (possibly empty) list of objects, and object , a class of loose multimorphisms.
- For each nonempty list of objects, and object , a class of tight multimorphisms.
- Maps , allowing tight multimorphisms to be viewed as loose ones.
- Tight identity multimorphisms .
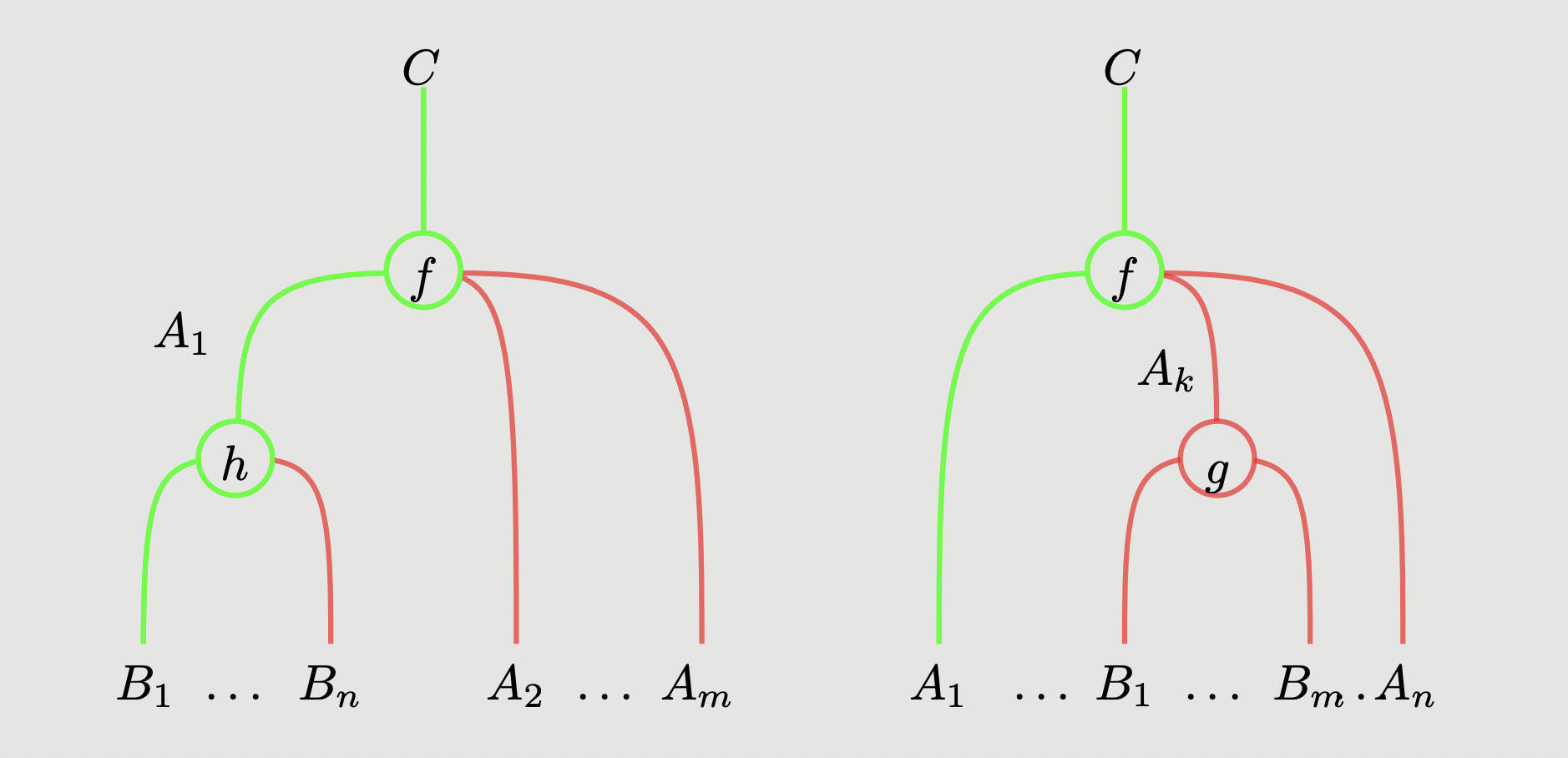
- Composition operations:
These are subject to equations, which we once again postpone until we set up our graphical calculus.
Warning: The graphical calculus for skew multicategories presented below, and representable skew multicategories presented later, is ongoing work, and a formal correspondence between the calculus and the theory of (left representable) skew multicategories is yet to be proven. The calculus can thus for the moment be taken as a pedagogical tool for the exposition of skew multicategories, and a formal proof of its correctness is left as future work.
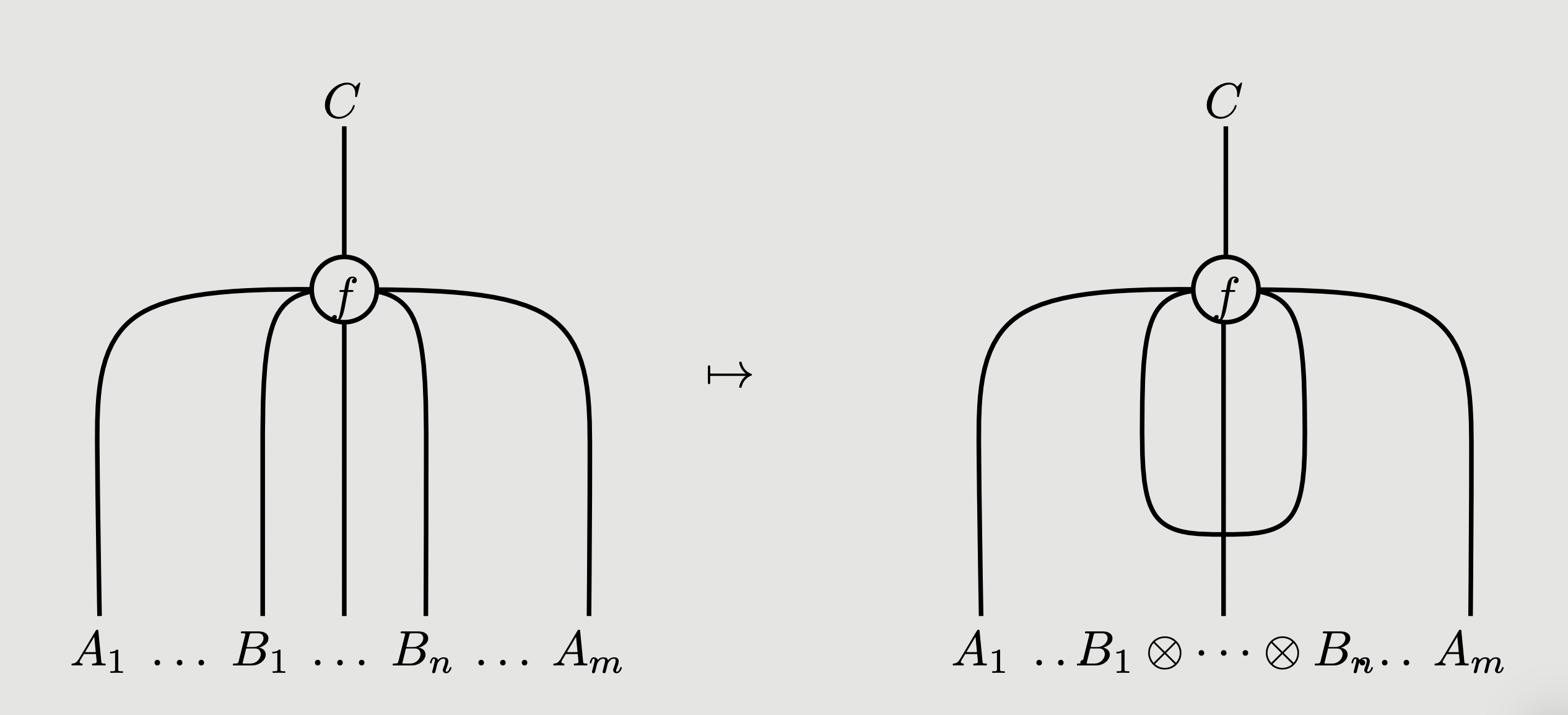
We graphically depict tight versus loose multimorphisms using two colours:
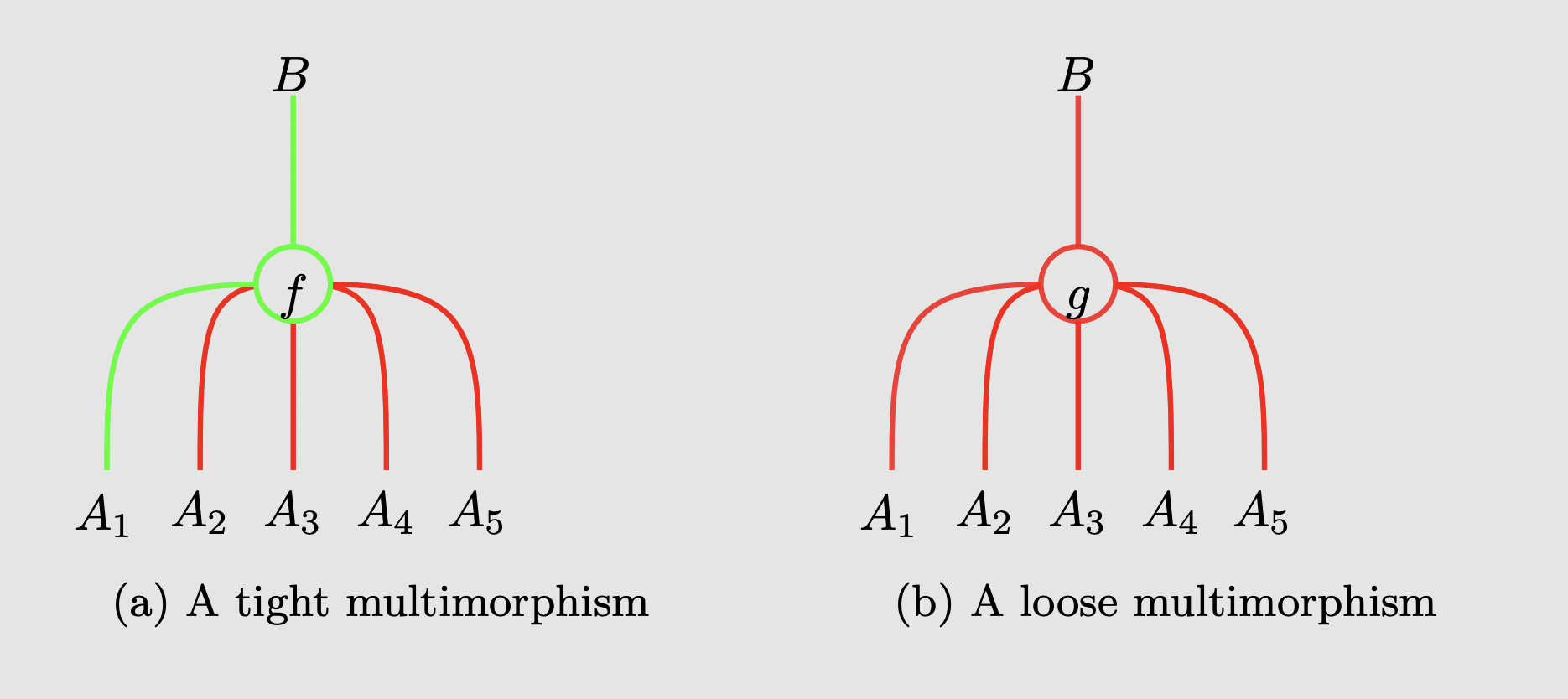
The placement of the colours ensures that the composition operations behave as above: for instance, the following ways of composing tight with tight multimorphisms, and tight with loose multimorphisms, yield tight multimorphisms:
Identities are depicted similarly:
While the map is represented as:
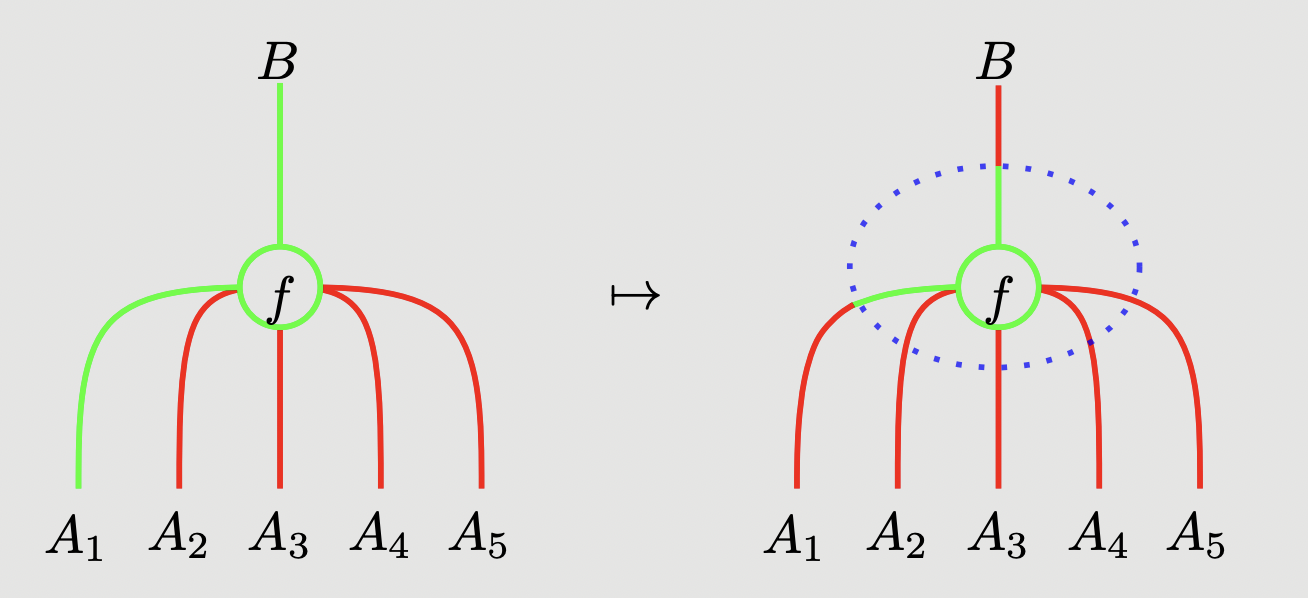
In addition to the equations holding by vitue of isotopy of diagrams, we also impose:
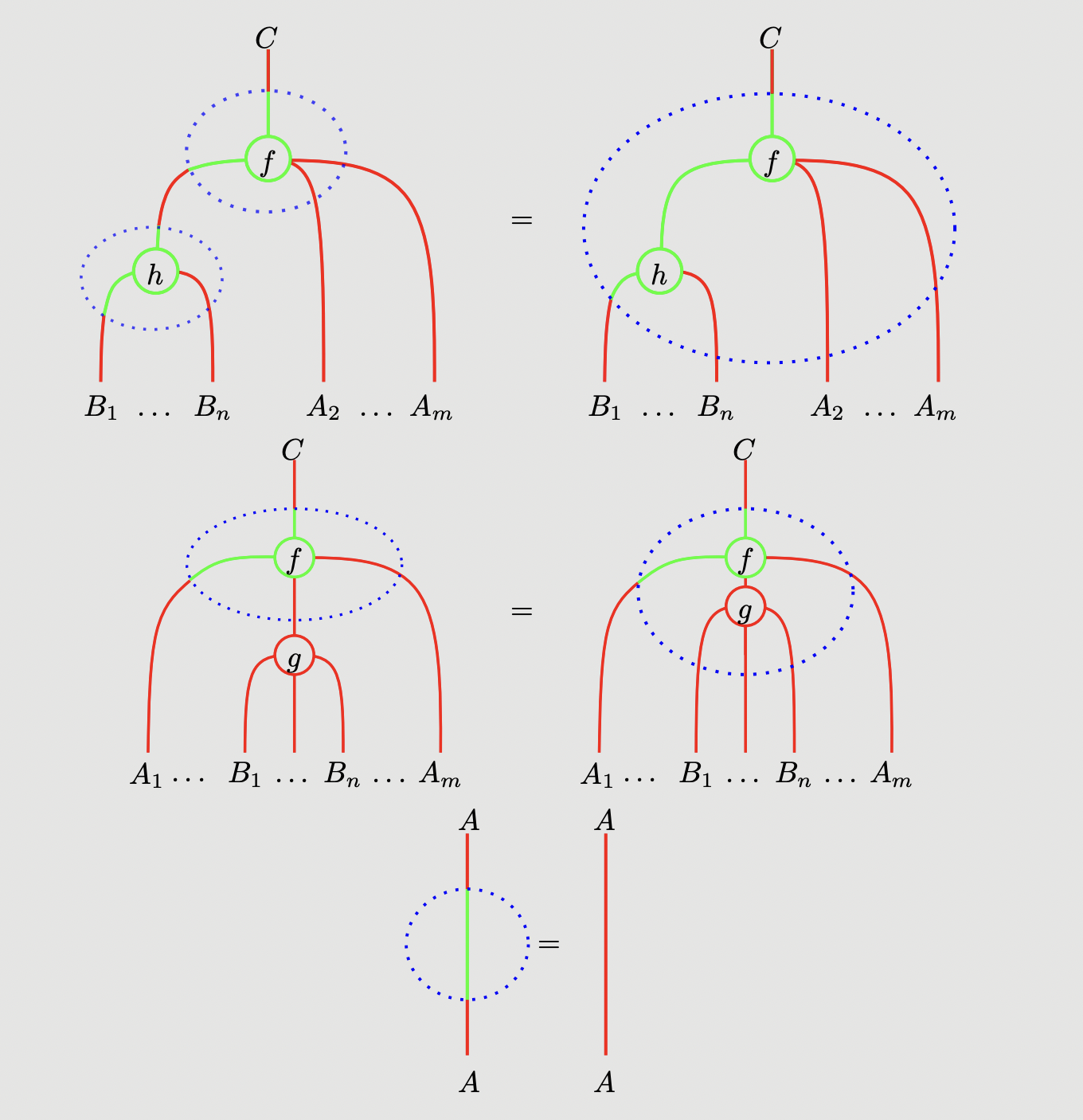
Once again, there is a relationship between skew-monoidal categories and skew multicategories. Given a skew-monoidal category , we define a skew-monoidal structure with:
- .
- .
- is defined by precomposition with .
The authors check that this gives a skew multicategory in (BL18).
Once again, the skew multicategories that arise from skew-monoidal categories in the above way can be characterised via a representability property:
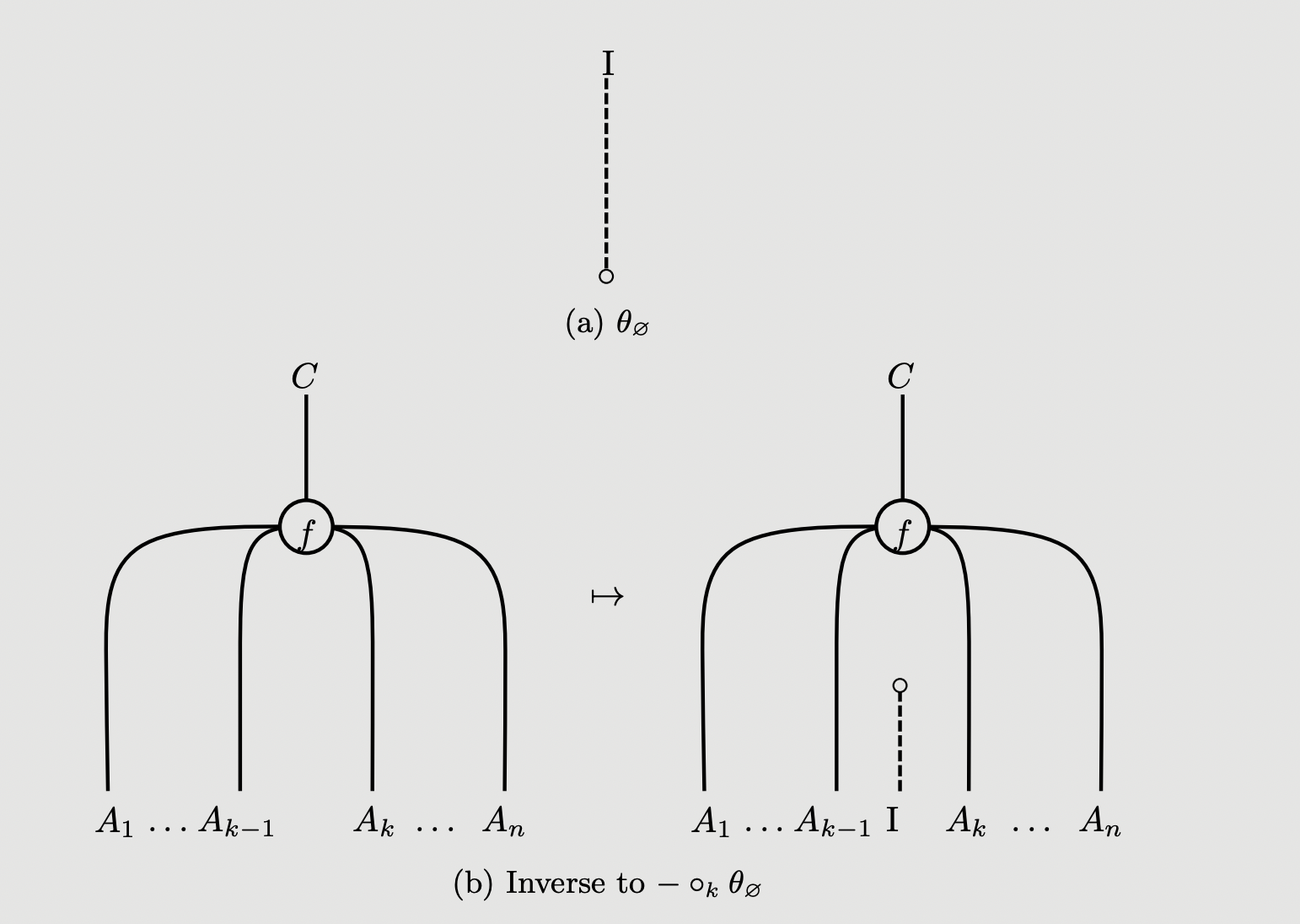
Definition: A skew multicategory is left representable if there is:
- An object , together with a loose morphism
- For every list of objects, an object together with a tight multimorphism such that the maps: are always invertible.
Once again, we depict and as:
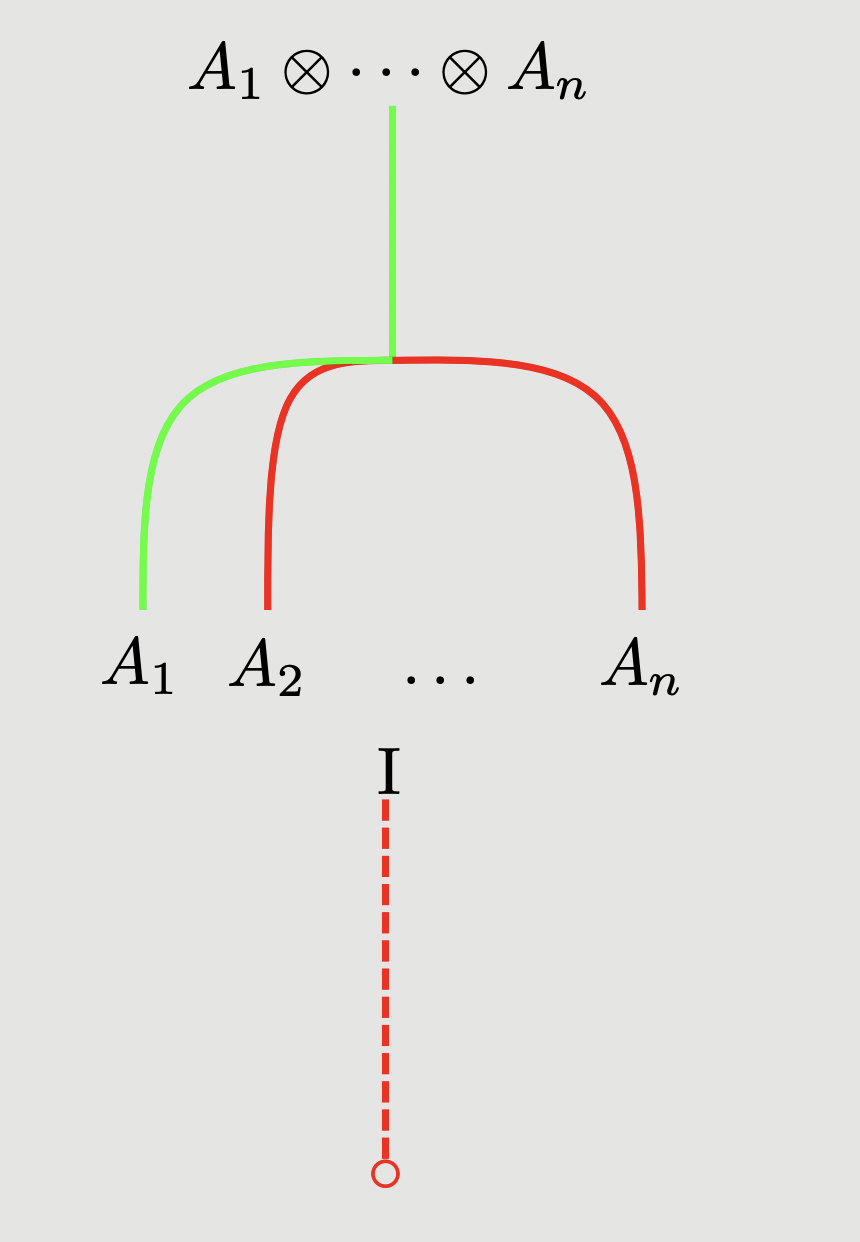
And the inverses to and as:
imposing the equations:
And we have the following:
Theorem: A skew multicategory is isomorphic to for some skew-monoidal category if and only if it is left representable.
implying correspondence between skew-monoidal categories and left representable skew multicategories.
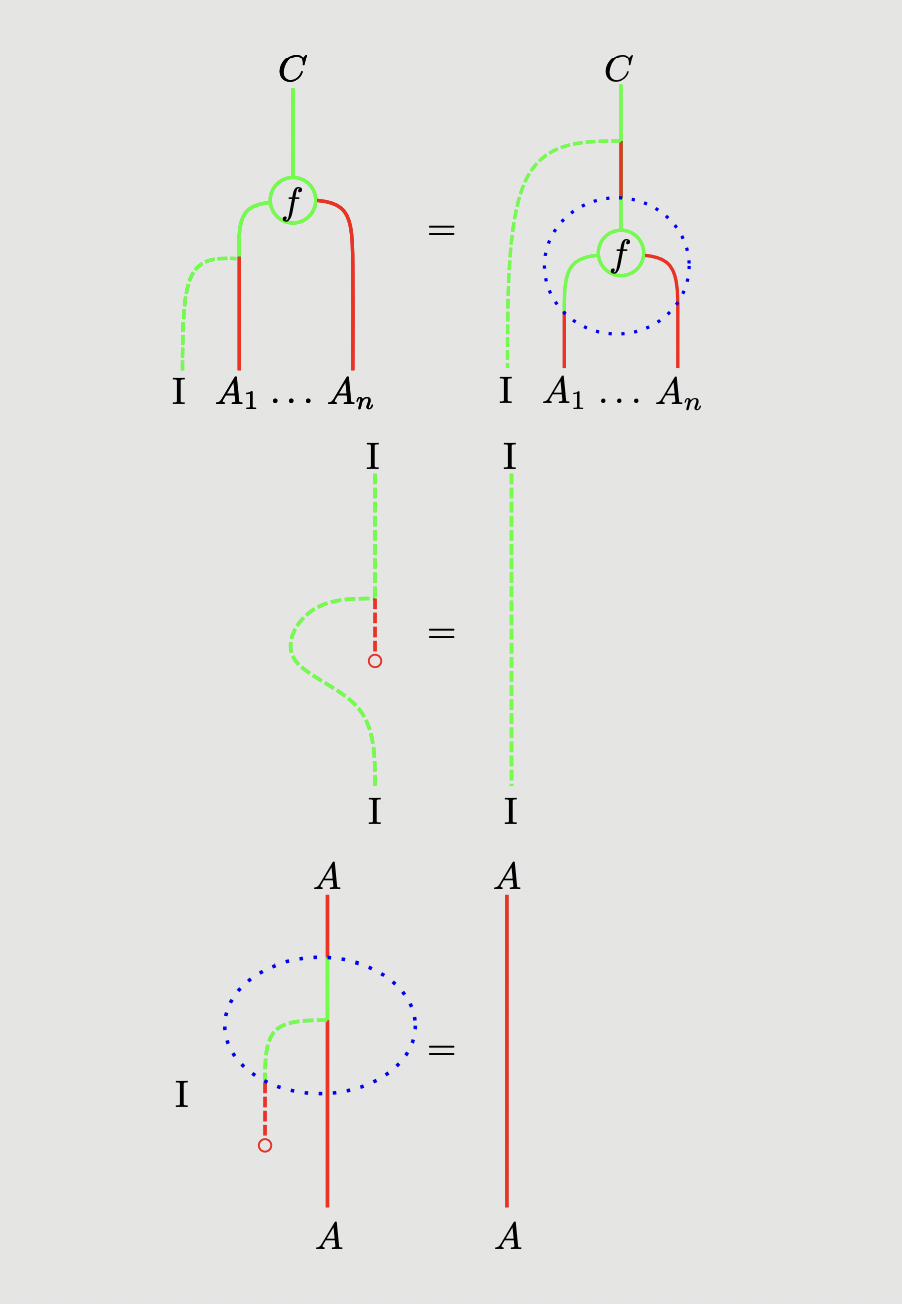
As a sanity check, we can construct the coherences , , and in our graphical calculus as:
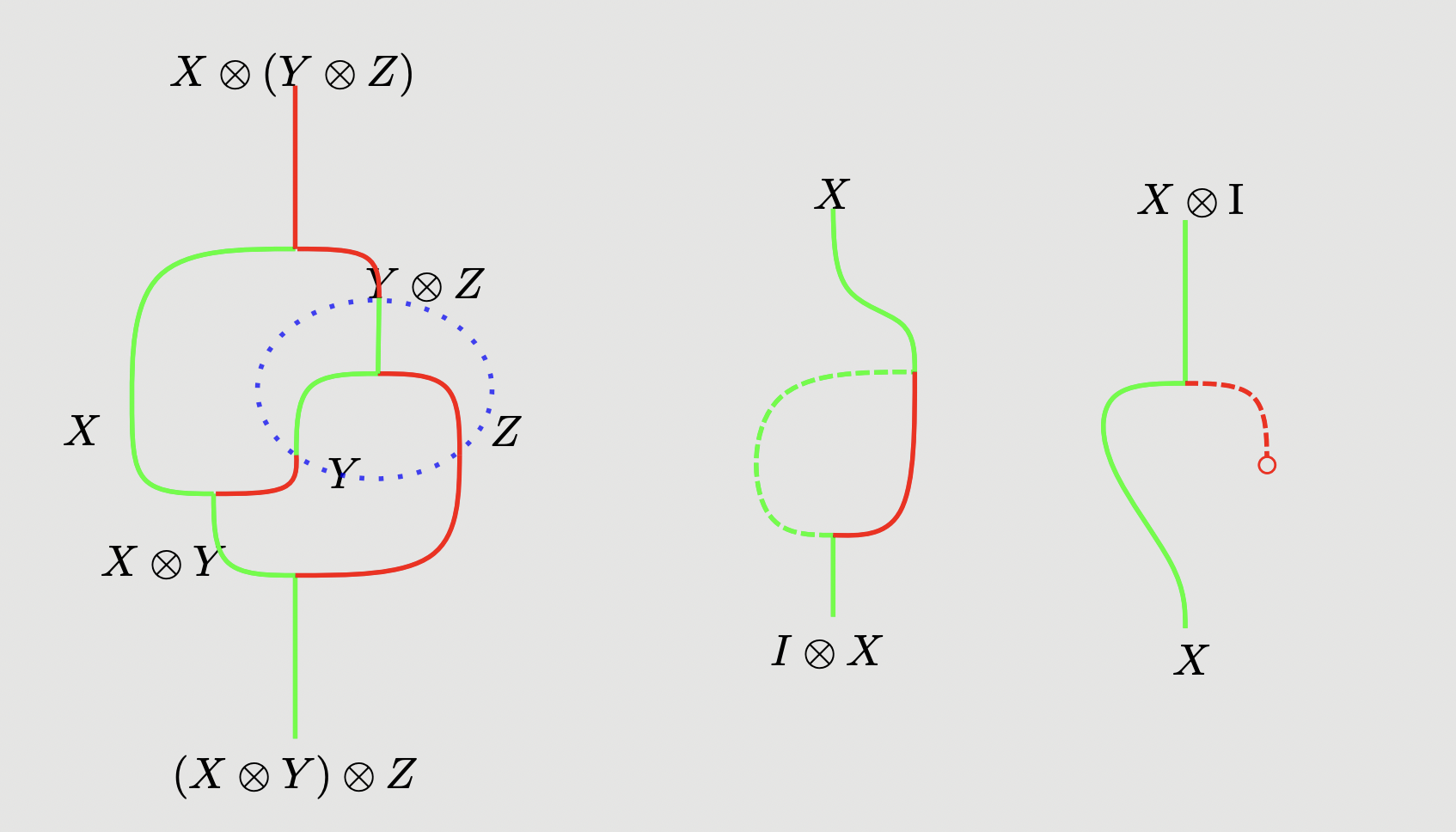
but now we cannot construct any diagrams of the opposite type!
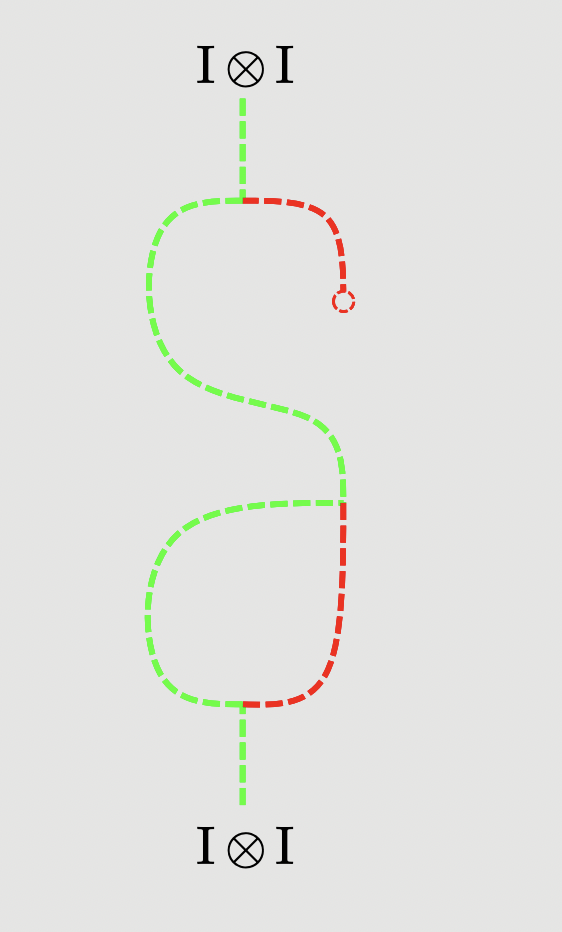
Modulo the warning given above, left representable skew multicategories and their graphical calculus now give us a way to understand and manipulate coherences in a free skew-monoidal category. While we no longer have uniqueness of diagrams of the same type, we now can get some visual intuition for why, for instance, :
Sequent Calculus for (Skew) Multicategories
While diagrammatic calculi like those presented above make reasoning intuitive and visual, the formal properties of such rewrite systems can be hard to rigorously understand and implement. A step towards an even more operational understanding of coherences in (skew-)monoidal categories is implementing their theory as a deductive system akin to those found in formal logic.
We present here the sequent calculus developed in (UVZ20) for (skew-)monoidal categories, which itself is inspired by the work of (BL18), and can be seen more explicitly as a calculus for left representable skew multicategories. First, we treat the ordinary (non-skew) case:
Definition: (Sequent Calculus for Multicategories) Fix an alphabet of object variables. The sequent calculus for multicategories has, as its judgements, sequents of the form , where . We use greek metavariables etc. for the lists of objects appearing on the left hand side. Its derivation rules are:
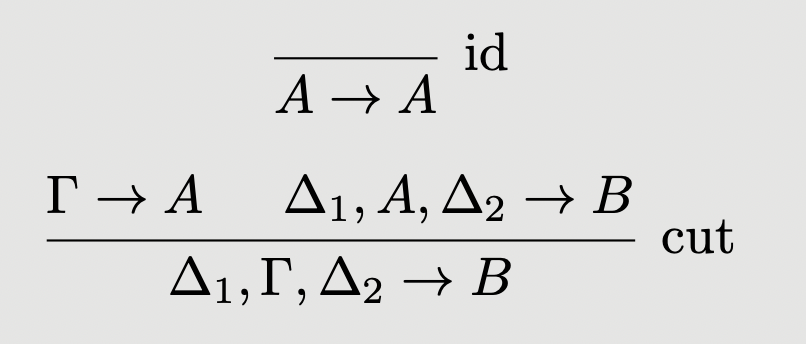
We identify derivations of the sequent calculus with morphisms in the free multicategory on . The above rules clearly correspond to the existence of identity morphisms, and composition in a multicategory. We must, however, impose associativity and unitality equations, for instance:
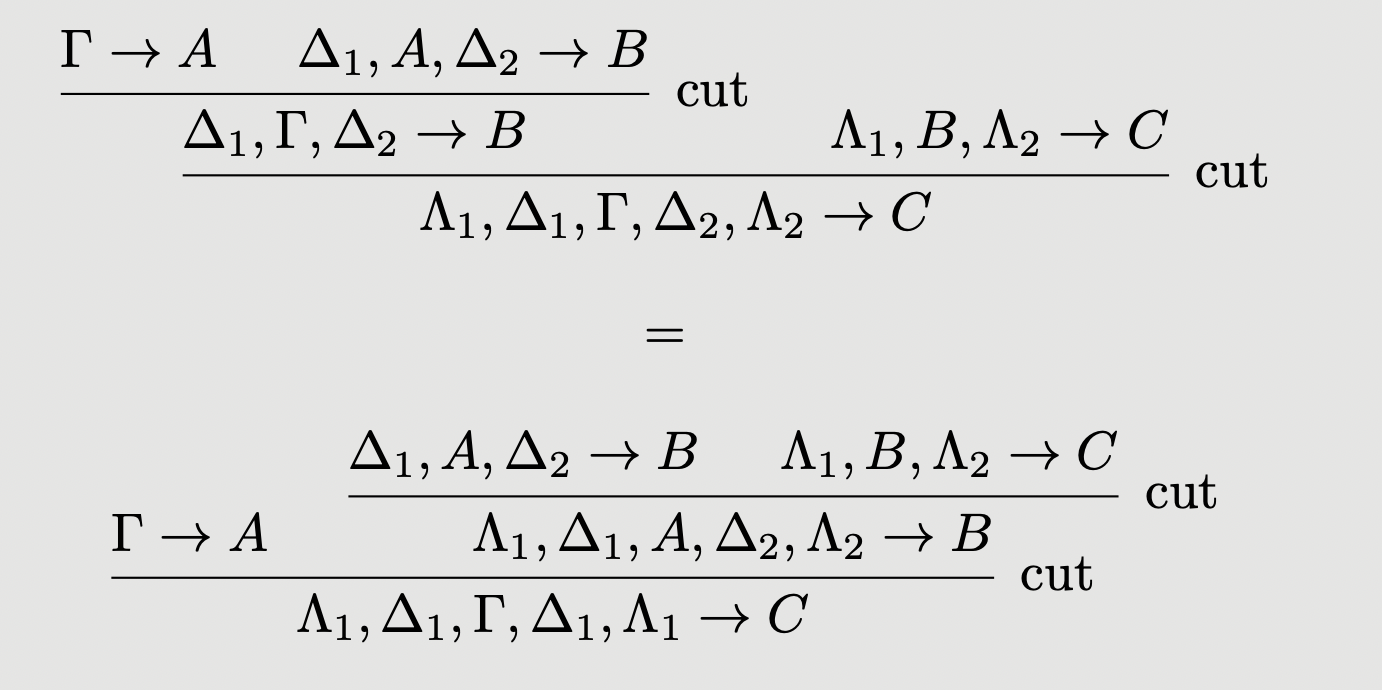
We omit the full rules: they can be easily derived from the axioms of a multicategory.
To capture the morphisms of a free representable multicategory, we must increase the expressive power. “Objects” appearing on each side of the sequent will no longer be simple variables, but now bracketed lists of variables delimited by , for instance , or , writing for the empty list. We add the following four rules:
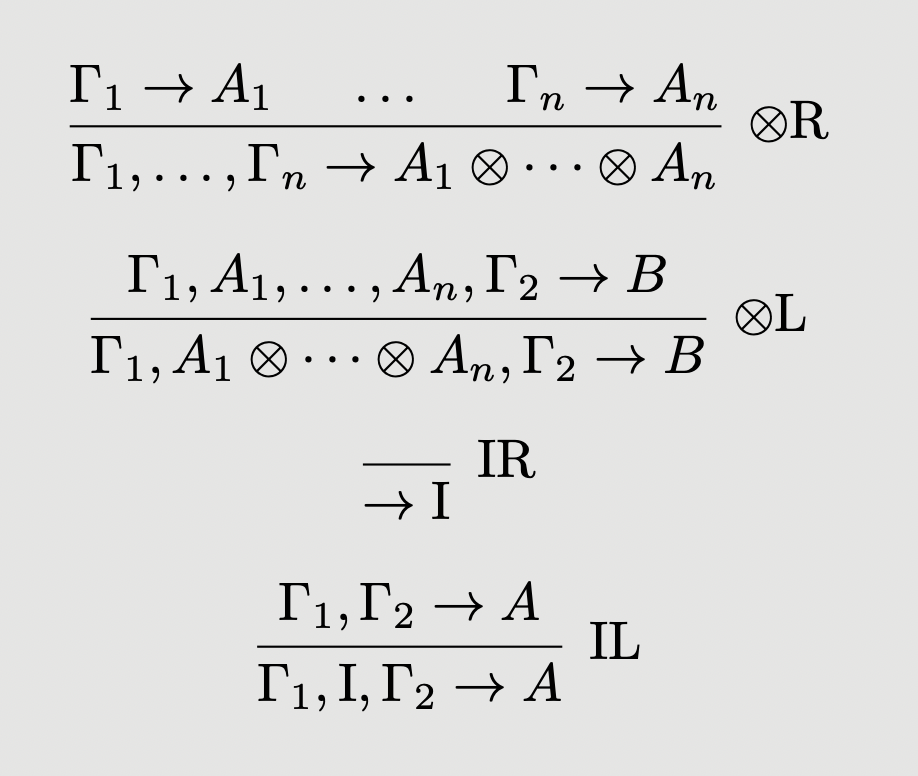
These can be interpreted as, respectively:
- R: the existence of the maps , coupled with composition.
- L: the inverses to
- R: the map
- L: the inverse to
and as such they are subject to more equations, similarly derived from the axioms of a representable multicategory. We have:
Theorem: There is a bijection between derivations of the above sequent calculus, up to the equational theory hinted at above, and the morphisms of a free representable multicategory (and hence a free monoidal category).
Moreover, these equations can be given a direction such that they implement a confluent rewriting system with unique normal forms of each type, giving another proof of theorem the coherence theorem.
The authors of (UVZ20) adapt the above sequent calculus to work for skew multicategories as follows. To capture the asymmetry inherent in the definition, judgements are now of the form , where is a list of objects as before, is an object, and is a “stoup”: a new privileged first position which can either be a single object, or empty (written in the second case). We will identify tight morphisms with derivations of sequents with nonempty stoup, and loose morphisms with derivations of sequents with empty stoup. We define:
Definition: (Sequent Calculus for Skew Multicategories) We replace the rules of the sequent calculus for multicategories with the following:
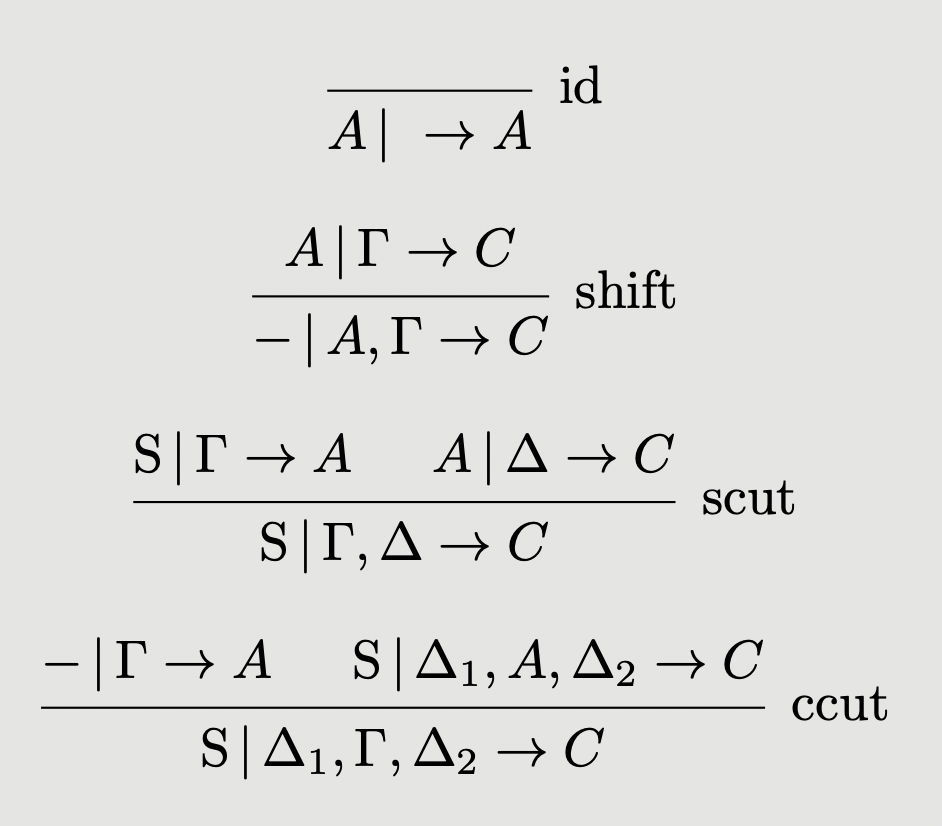
which correspond, respectively, to:
- (tight) identity morphisms,
- the map ,
- composition
- composition
These are again subject to equations which are listed in full in (UVZ20), based on the axioms of skew multicategories. For instance, the equation expressing compatibility of with composition becomes:
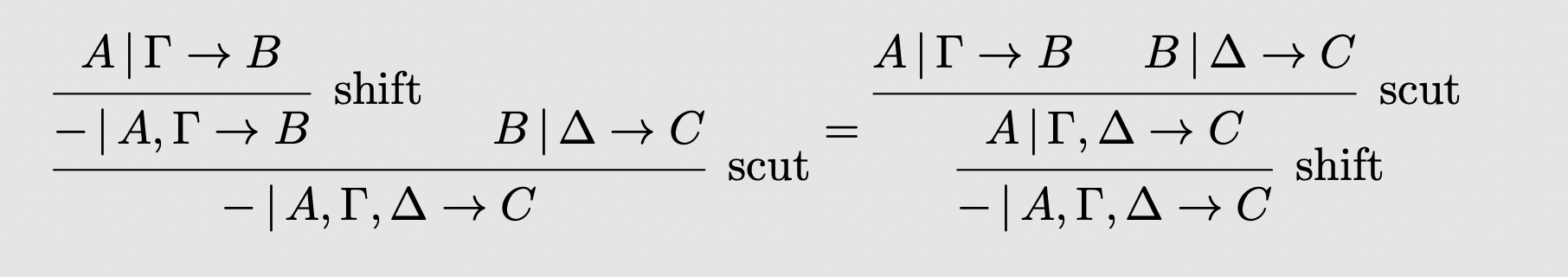
To augment this into a sequent calculus for left representable skew multicategories, we once again add four new rules, which now make key use of the stoup:
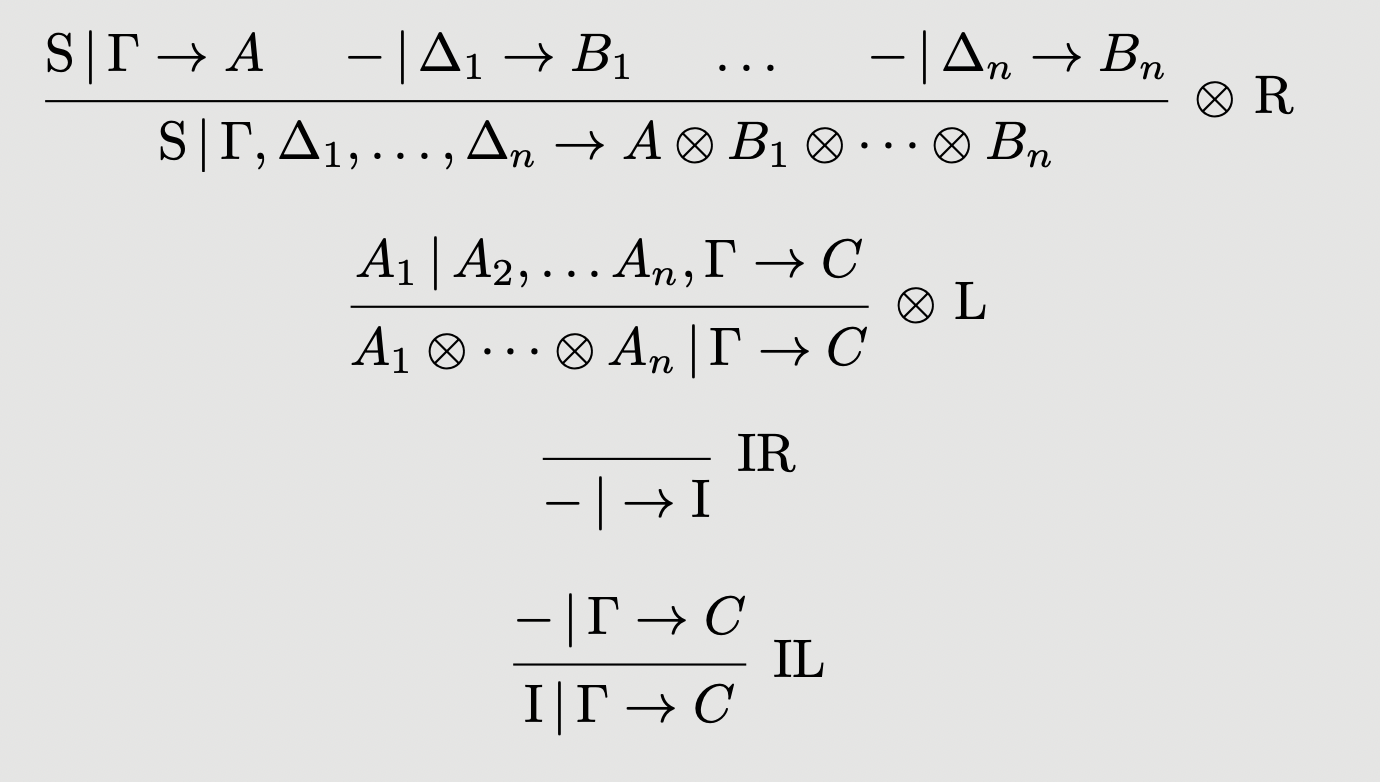
These correspond to:
- Composition with the maps
- The inverse to
- The map
- The inverse to
And are subject to rules listed in (UVZ20). This finally gives us:
Theorem: There is a bijection between derivations of of the above sequent calculus, up to the equational theory given in (UVZ20), and tight morphisms of a free left representable skew multicategory. In the case where , we have that derivations of up to the equational theory are in bijection with morphisms from to in a free skew-monoidal category.
For instance, a derivation corresponding to the associator is:
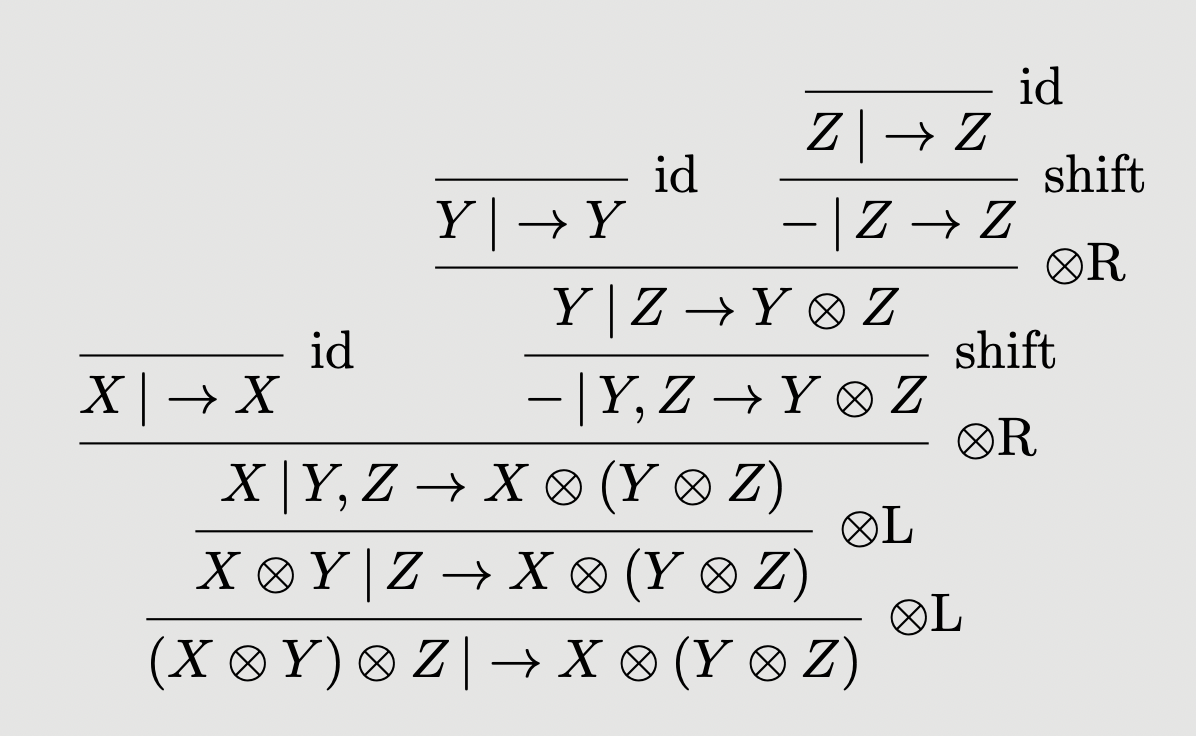
Moreover, the authors show that these equational rules can be directed, giving a confluent terminating rewriting system, and thus equality of coherences in a skew-monoidal category can be decided using the above logical system.
What’s more, we may be interested in asking whether there exists a coherence morphism between two objects, and enumerating such morphisms. The authors in (UVZ20) also provide an algorithm to do this, by adapting the above sequent calculus to a so-called “focused” version.
Conclusion and future work
While the coherence theorem of MacLane no longer holds for skew-monoidal categories, rewriting approaches like those investigated above can provide a way to get to grips with these complex structures. There is much more room for investigation of related structures, such as skew-closed categories, and braided skew-monoidal categories, where the above approaches could also be fruitful. In addition, there is future work in a more rigorous analysis of the graphical calculus presented above for skew-monoidal categories.
References
{#UVZ20} [[Tarmo Uustalu, Niccolò Veltri, Noam Zeiberger]], The Sequent Calculus of Skew Monoidal Categories 2020 (arXiv:2003.05213)
{#Oli23 [[Federico Olimpieri]], Coherence by Normalization for Linear Multicategorical Structures 2023 (arXiv:2302.05755)
{#WGZ22} [[Paul Wilson, Dan Ghica, and Fabio Zanasi]], String diagrams for non- strict monoidal categories 2022 (arXiv:2201.11738)
{#Mac63} [[Saunders Maclane]], Natural Associativity and Commutativity 1963 (pdf)
{#Lei03} [[Tom Leinster]], Higher Operads, Higher Categories 2003 (arXiv)
{#BL18} [[John Bourke and Stephen Lack]], Skew monoidal categories and skew multicategories 2017 (arXiv:1708.06088)

Re: Skew-Monoidal Categories: Logical and Graphical Calculi
It’s great to get a string diagram framework and sequent calculus up and running for skew monoidal categories. Thanks for this post!
The links to references in the article don’t work, and the references look funny. I’ve rarely if ever used links within -Category Café articles, so I forget how it works.