The n-Category Café

Imagine a frog in pond with a $100$ lily pads, which form a $10$ by $10$ grid. Suppose that the frog sits on a lily pad and can only make jumps of one unit i.e. the frog can jump forwards, backwards, left or right.

Let $Q$ be the set of lily pads. Let $q_0$ be the lily pad the frog currently is sitting on and let $q_1$ be the lily pad the frog wants to go to. Let $A$ be the set of symbols $\{f,b,l,r\}$. A jump forward corresponds to an input of $f$ and to the map $\tau_f:Q\to Q$ moving the frog forward (if possible) in the grid. Similarly, the symbols $b,l$ and $r$ with respective maps $\tau_b,\tau_l$ and $\tau_r$ correspond to jumps backwards, left and right, whenever these are possible. The data $(Q,q_0,\{q_1\},A, (\tau_a)_{a\in A})$ form a finite deterministic automaton.

The transition maps in the definition of a finite deterministic automaton are morphisms in $\mathbf{FinSet}$, the category of finite sets and functions. We can generalize the idea of a finite deterministic automaton, by letting the transition maps be morphisms in more general categories. In particular we will look at Kleisli categories of monads on $\mathbf{FinSet}$ or $\mathbf{Set}$.

If the transition map is a map in the Kleisli category of the powerset monad, i.e. functions $M_a:Q\to\mathcal{P}(Q)$, we obtain finite non-deterministic automata. In our example that would mean that the frog can choose between a set of different jumps for a given input. If the frog is sitting on lily pad $q$, then $\tau_f(q)$ is the set of all reachable lily pads that are in front of the frog.

If we let the transition map be a morphism in the Kleisli category of the monad of finitely supported measures on $\mathbf{Set}$, we obtain weighted automata and if the transition map is a morphism in the Kleisli category of the distribution monad, we obtain Markov automata. In the case of the frog this would mean that the frog prefers some lily pads over others and this preference is given in terms of distributions. If the frog sits on lilypad $q$, then $\tau_f(q)$ is a distribution on the reachable lily pads in front of the frog.

In the following, we will first consider categories of Markov automata as presented in The compositional construction of Markov process II by Albasini, Sabadini, and Walters and then generalize this to $T$-automata for commutative strong monads $T$ on a monoidal category $\mathcal{C}$. We will study categories where the morphisms are these generalized automata and look at the monoidal structure and properties this category inherits from $\mathcal{C}$ and $\mathcal{C}_T$.

Markov Automata

Here, we will consider a definition of automata that deviates from the classical literature. A Markov automaton $Q^X_{Y;A,B}$ consists of the following data:

• A set of states also denoted $Q$.

• Two sets of parallel interfaces $A$ and $B$ (playing the role of inputs/signals)

• Two sets of sequential interfaces $X$ and $Y$ together with functions $\gamma_Q:X\to Q$ and $\delta_Q:Y\to Q$ in $\mathcal{C}$ (playing the role of start/stop states)

• Transition matrices indexed by the parallel interfaces $Q_{a,b}$ such that for all $q \in Q$ $$\sum_{q'\in Q} \sum_{a\in A, b\in B} Q_{a,b} = 1$$

Markov automata form a symmetric monoidal category in two distinctly different ways: one in which we compose automata in parallel and one in which we compose in sequence.

Parallel Composition

Let $\mathbf{ParAut}$ be the category with

• objects as finite sets $A,B,C,\dots$

• morphisms $A \to B$ as weighted automata whose parallel interfaces are the sets $A$ and $B$.

The parallel composite of morphisms $A \to B \to C$ is defined to be the weighted automaton with states $Q \times R$ and whose top and bottom interfaces are the respective set products $X \times Z$ and $Y \times W$ with sequential interface functions $\gamma_Q \times \gamma_R$ and $\delta_Q \times \delta_R$. The parallel interfaces are $A$ and $C$ with transition matrices defined by

$$(Q||R)_{a,c} = \sum_{b\in B} Q_{a,b} \otimes R_{b,c}$$

where $\otimes$ denotes the Kronecker product of matrices. This is shown diagrammatically in the figure below.

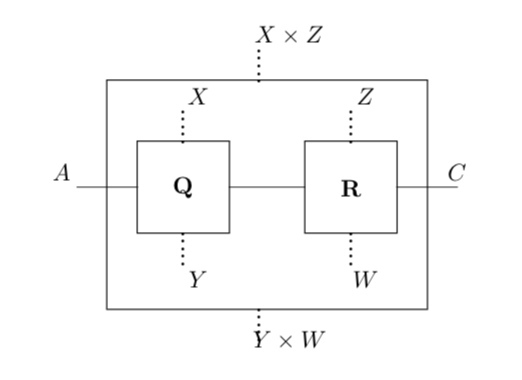
The tensor product of two objects $A$ and $B$ in $\mathbf{ParAut}$ is their cartesian product $A\times B$. On morphisms $Q^X_{Y;A,B}$ and $R^Z_{W;C,D}$, the tensor product has as states $Q \times R$, transition matrices

$$(Q \times R)_{(a,c),(b,d)} = Q_{a,b} \otimes R_{c,d},$$

and $X \times Z$ and $Y \times W$ as sequential interfaces with interface functions $\gamma_Q \times \gamma_R$ and $\delta_Q \times \delta_R$ respectively. Note that the identity object $I = \{ *\}$ is the one element set.

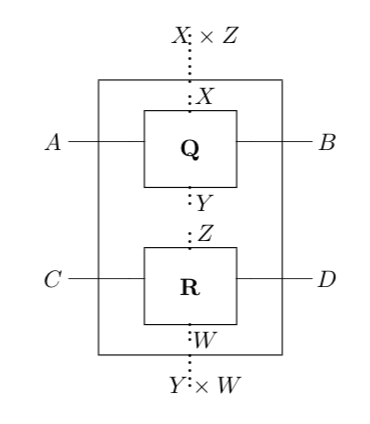
To show $\mathbf{ParAut}$ is symmetric, we will use the fact that there is a monoidal functor

$$\text{Par} : \mathbf{Rel} \to \mathbf{ParAut}$$

on the symmetric monoidal category of (finite) sets and relations $\mathbf{Rel}$. This functor acts as the identity on objects $\text{Par}(A) = A$ and on morphisms $R \subseteq A \times B$ by associating $R$ to the following automaton:

• Each of the sequential interfaces and state space are the singleton set $X=Y=Q=\{*\}$.

• The left and right parallel interfaces are $A$ and $B$ respectively and the transition matrices (in this case numbers) are given by $$\text{Par}(R)(a,b)_{\ast,\ast} = \begin{cases} 1, & (a,b) \in R \\ 0, & \text{otherwise} \end{cases}$$

for $a \in A$ and $b \in B$. Symmetry in $\mathbf{ParAut}$ then follows from $\text{Par}$ being a monoidal functor. Using this technology we will show some nice properties of $\mathbf{ParAut}$ by pushing them forward through $\mathbf{Rel}$.

Proposition. $\mathbf{ParAut}$ is compact closed.

This in particular allows us to define the notion of feedback. To show that $\mathbf{Rel}$ (and hence $\mathbf{ParAut}$) is compact closed we instead show that each object in $\mathbf{Rel}$ is a Frobenius algebra and apply the following lemma.

Lemma. If an object $A$ in a monoidal category forms a Frobenius algebra then it is dual to itself.

Let $\Delta_A : A \to A \times A$ be the diagonal map, thought of as a morphism in $\mathbf{Rel}$ and $p_A : A \to 1$ the unique morphism to the terminal object. Moreover given a morphism $R$, let $R^{\text{op}}$ denote the opposite relation (by simply reversing the arrow). Then the monoid structure for the Frobenius algebra of an object $A$ in $\mathbf{Rel}$ is given by $(A,\Delta_A^{\text{op}},p_A^{\text{op}})$ and, dually, the comonoid structure by $(A, \Delta_A,p_A)$.

Sequential Composition

Let $\mathbf{SeqAut}$ be the category with

• objects as finite sets $X,Y,Z \dots$

• morphisms $X \to Y$ as weighted automata

$Q^X_{Y;A,B}$ whose sequential interfaces are the sets $X$ and $Y$.

We define the sequential composite of two morphisms $Q^X_{Y;A,B}$ and $R^Y_{Z;C,D}$ to be the weighted automaton $Q \circ R$ whose states are given by the disjoint union $(Q + R)/\sim$ quotiented by the relation $\delta_Q(y) \sim \gamma_R(y)$. The parallel interfaces are $A+C$ and $B+D$ and top and bottom interfaces are $X$ and $Z$ with the respective interface functions

$$\begin{array}{cc} \gamma &: X \to Q \to Q + R \to (Q+R)/\sim \\ \delta &: Z \to R \to Q + R \to (Q+R)/\sim. \end{array}$$

If we let $q,q' \in Q$ and $r,r' \in R$ and $[s]$ denote the equivalence class of state $s$ in $Q + R$, then the transition matrices are given by

$$\begin{array}{cc} [(Q \circ R)_{a,b}]_{[q],[q']} &= \sum_{s \in[q], s'\in [q']} [Q_{a,b}]_{s,s'} \\ [(Q \circ R)_{c,d}]_{[r],[r']} &= \sum_{s \in[q], s'\in [q']} [Q_{a,b}]_{s,s'} \end{array}$$

where all other entries are zero. This is shown diagrammatically below.

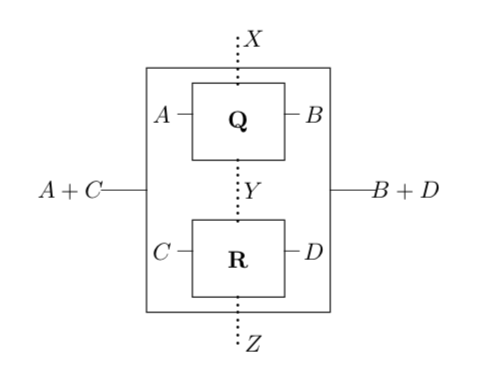
The tensor product of $Q^X_{Y;A,B}$ and $R^Z_{W;C,D}$ has states $Q + R$ without any quotienting. The parallel interfaces are again $A+C$ and $B+D$ while top and bottom interfaces $X + Z$ and $Y + W$ have interface functions $\gamma_Q + \gamma_R$ and $\delta_Q + \delta_R$. The transition matrices are given by $$\begin{array}{cc} [(Q + R)_{a,b}]_{q,q'} &= [Q_{a,b}]_{q,q'} \\ [(Q + R)_{c,d}]_{[r],[r']} &= [Q_{c,d}]_{r,r'} \end{array}$$ where all other entries are again zero.

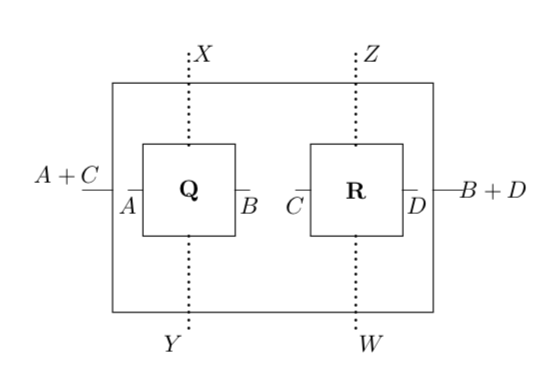
Just as in the case of $\mathbf{ParAut}$, one can show $\mathbf{SeqAut}$ is a compact closed symmetric monoidal category by defining a monoidal functor $\text{Seq} : \mathbf{Rel} \to \mathbf{SeqAut}$.

$T$-Automata

We now generalize the preceding categories to work with a commutative strong monad. Let $(\mathcal{C},\otimes,I)$ be a (strict) symmetric monoidal category and let $(T,\mu,\eta)$ be a commutative monad on $\mathcal{C}$ with strength $\sigma$. Let $\mathcal{C}_T$ be the Kleisli category of this monad. The strength induces a monoidal structure on $\mathcal{C}_T$ (see Folklore: Monoidal kleisli categories). We will denote the tensor product and unit object on $\mathcal{C}_T$ also by $\otimes$ and $I$.

Definition. A $T$-automaton consists of

• an object $Q$ in $\mathcal{C}$,

• morphisms $\gamma_Q:X\to Q$ and $\delta_Q:Y\to Q$ in $\mathcal{C}$ (sequential interfaces) and

• objects $A$ and $B$ in $\mathcal{C}$ (parallel interfaces) together with a map $M_Q:Q\otimes A\rightsquigarrow Q\otimes B$ in $\mathcal{C}_T$ (transition morphisms).

Parallel composition

Consider two $T$-automata $\mathcal{Q}:=(Q,\gamma_Q,\delta_Q,M_Q:Q\otimes A\rightsquigarrow Q\otimes B)$ and $\mathcal{R}:=(R,\gamma_R,\delta_R,M_R:R\otimes B\rightsquigarrow R\otimes C)$.

The parallel composite of $\mathcal{R}$ and $\mathcal{Q}$ is given by the $T$-automaton $$\mathcal{Q}\circ_p\mathcal{R}:=\big(Q\otimes R,\gamma_Q\otimes \gamma_R,\delta_R\otimes \delta_Q, (1_R\otimes M_Q)\diamond (1_Q\otimes M_R)\big),$$ where $\diamond$ is used to mean composition in $\mathcal{C}_T$.

Let $\mathbf{ParAut}(T)$ be the category that has the same objects as $\mathcal{C}$ and where a morphism from $A$ to $B$ is a $T$-automaton whose parallel interfaces are given by $A$ and $B$ and where composition is given by parallel composition.

Given two $T$-automata $\mathcal{Q}:=(Q;\gamma_Q,\delta_Q,M_Q:Q\otimes A\rightsquigarrow Q\otimes B)$ and $\mathcal{R}:=(R,\gamma_R,\delta_R,M_R:R\otimes C \rightsquigarrow R\otimes D$, we can form a new $T$-automaton $$\mathcal{Q}\otimes_p\mathcal{R}:=(Q\otimes R, \gamma_Q\otimes \gamma_R,\delta_R\otimes \delta_Q, M_Q\otimes M_R),$$ which we call the parallel tensor product. The parrallel tensor product $\otimes_p$ together with the object $I$ define a monoidal structure on $\mathbf{ParAut}(T)$.

We will now define a (strict) monoidal functor $$\text{Par}:\mathcal{C}_T\to \mathbf{ParAut}(T)$$ The functor acts as the identity on objects and sends a morphism $A\rightsquigarrow B$ in $\mathcal{C}$ to the $T$-automaton $$(I,\text{Id}_I,\text{Id}_I, \text{Id}_I\otimes f).$$

Because the monoidal structure on $\mathcal{C}$ is symmetric, so is the monoidal structure on $\mathbf{ParAut}(T)$ using the monoidal functor $\text{Par}$.

Note that $\text{Par}$ sends Frobenius algebras to Frobenius algebras and is surjective on objects.

Proposition. If $\mathcal{C}_T$ is compact closed, so is $\mathbf{ParAut}(T).$

Remark. We have tried to also generalize the sequential operations to $T$-automata, but we will leave the details of this construction for future work.

Examples

Consider the following game in a casino: the player is asked to place a bet, let’s say the player decides to place a bet of £$a$. After the bet is placed, the dealer blindly picks a coin from a bag of (fair and unfair) coins; suppose the dealer picks coin $b$, which has probability $p$ on heads. Then the dealer flips the coin. If coin lands on heads, the player wins £$a$. If it falls on tails, the player loses the placed bet of £$a$.

We represent the bank balance of the player by $Q:=\{0,1,\ldots, N\}$. We furthermore suppose that the player enters the casino with £$x$ and has decided to leave the casino when their bank balance reaches states in $Y\subseteq Q$.

If we let $A$ to be the set of possible bets, i.e. $A:=\{0,1,\ldots,N\}$ and let $B$ be the bag of coins the dealer picks from. For a coin $b\in B$, we denote the probability on heads by $p_b$. For a bet $a\in A$ and a bank balance of $q$ such that $q\geq a$, let $M(a,q)$ be the measure on $B\times Q$ defined by $$(b,q')\mapsto \begin{cases}p_b & \text{ if }q'=q+a\\ 1-p_b & \text{ if }q'=q-a\\ 0 & \text{ otherwise.}\end{cases}$$ This measures the chance of moving from a bank balance of $q$ to a balance of $q'$ when playing the game.

For a bet $a$ and a bank balance of $q$ such that $q < a$, let $M(a,q)$ be the measure on $B\times Q$ defined by

$$(b,q')\mapsto \begin{cases}1 & \text{ if }q=q'\\ 0 & \text{ otherwise,}\end{cases}$$

as the player is not allowed to bet more money than they have.

This defines the Kleisli map $Q\times A\rightsquigarrow Q\times B$ and the data $(Q,x,Y,M)$ form a weighted automaton. Note that $0\in Q$ is a so called deadlock state, since the player’s bank balance won’t change anymore after reaching $0$. In particular, if $0$ is not an element of $Y$, the player will have to keep playing the game forever.

Suppose now that the casino has multiple tables with different bags of coins and suppose that two friends go to the casino together. Then parallel compositions combines the information of the two friends playing at the same table, i.e. the game is played with the same coin. The parallel product and the sequential sum both combine the information of the two friends playing at different tables. The product measures the chance that person 1 reaches state $q'$ and that person 2 reaches state $r'$, while the sum measures the chance that that person 1 reaches state $q'$ or that person 2 reaches state $r'$.

If the player starts with £$x$ and decides to move to a different table when reaching £$y$ and to stop playing when their bank balance is £$z$, we can model the combination of the two games with the sequential composition.