Counting Points on Elliptic Curves (Part 1)
Posted by John Baez
You’ve probably heard that there are a lot of deep conjectures about -functions. For example, there’s the Langlands program. And I guess the Riemann Hypothesis counts too, because the Riemann zeta function is the grand-daddy of all -functions. But there’s also a million-dollar prize for proving the Birch-Swinnerton–Dyer conjecture about -functions of elliptic curves. So if you want to learn about this stuff, you may try to learn the definition of an -function of an elliptic curve.
But in many expository accounts you’ll meet a big roadblock to understanding.
The -function of elliptic curve is often written as a product over primes. For most primes the factor in this product looks pretty unpleasant… but worse, for a certain finite set of ‘bad’ primes the factor looks completely different, in one of 3 different ways. Many authors don’t explain why the -function has this complicated appearance. Others say that tweaks must be made for bad primes to make sure the -function is a modular form, and leave it at that.
I don’t think it needs to be this way.
For example, Wikipedia defines the -function of an elliptic curve this way:
where where in the case of good reduction is (number of points of mod ), and in the case of multiplicative reduction is ±1 depending on whether E has split (plus sign) or non-split (minus sign) multiplicative reduction at . A multiplicative reduction of curve by the prime is said to be split if is a square in the finite field with elements.
I won’t list all the ways this is confusing and unpleasant. The article doesn’t say what is! I won’t either. I’ll just say that ranges over primes and is a number called the conductor of the elliptic curve. If you follow the link and read Wikipedia’s explanation of that, you’ll enter a whole new world of pain.
Surely this can’t be the fundamental definition of the -function of an elliptic curve! How could such a messy, complicated thing be fundamental? Surely this should be a theorem, where we take some simpler definition and grind out its consequences in gory detail.
I won’t actually give you what I think is a better definition of the -function of an elliptic curve. Sorry! I might someday, but I still need to check that it matches this definition.
As a small step in this direction, let’s unpack the mysteries of the ‘conductor’ and transform the above definition into something easier to understand. The definition will still be extremely unpleasant. But it will involve some nice concepts about curves.
For our purposes let’s start with a lowbrow definition of an elliptic curve. Take an equation
where is any cubic with integer coefficients. If does not have repeated complex roots, we call this an elliptic curve. The solutions will form a smooth manifold, and in fact a smooth affine variety. If we tack on one extra point, a so-called ‘point at infinity’, we get a smooth projective variety that’s shaped like a torus.
What if has repeated roots? Then the solutions will not form a smooth variety. Two things can go wrong: we can get a cusp, or a node. For example,
has a cusp at the origin:
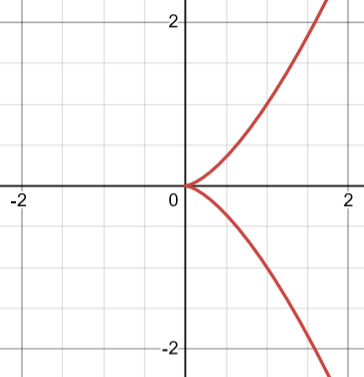
The cusp is the sharp pointy thing.
On the other hand,
has a node at the origin:
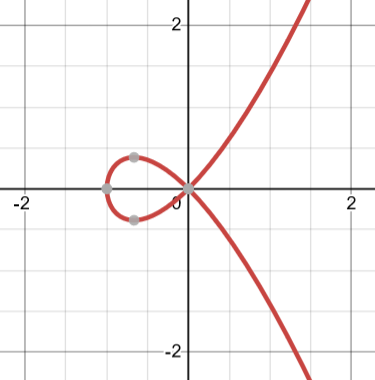
There’s a node where the curve crosses itself. Near the node the curve looks like a little X. In other words, there are two different tangent lines at a node.
So far I’ve been talking about complex solutions of
and drawing you real solutions. But because has integer coefficients, we can look at solutions in any field whatsoever! The -function of an elliptic curve is a clever way of keeping track of how many solutions there are in every finite field. There’s one finite field for each prime power .
The horrible definition of -function given above only talks about the finite fields , not the other finite fields involving powers of primes. That’s one reason it’s forced to be tricky and complicated. It’s trying to be ‘economical’, but premature economizing is one of the main causes of suffering in mathematics.
Okay, now let me unpack the above definition of -function:
The -function of an elliptic curve is defined to be where:
1) if has good reduction at . This means that our elliptic curve remains smooth if we treat it as a curve over .
2) if has additive reduction at . This means that gets a cusp if we treat as a curve over .
3) if has split multiplicative reduction at . This means that we gets a node if we treat as a curve over , and the two tangent lines to this node have slopes that are defined in .
4) if has nonsplit multiplicative reduction at . This means that we gets a node if we treat it as a curve over , but the two tangent lines to this node have slopes that are not defined in .
It’s still an annoying definition by cases, where each case involves an arbitrary-looking formula. Whenever a definition involves different cases, you should assume someone hasn’t precisely put their finger on the concept they’re after… or else they don’t want to tell you about it.
And of course we need purely algebraic definitions of ‘smooth’, ‘cusp’ and ‘node’ that work for algebraic curves over finite fields, for this definition to even make sense. But that’s what algebraic geometers are paid to do, so we can assume that’s been done.
More confusing to me was case 4). What the heck is a line whose slope is not defined? Here’s the deal: when you try to work out the slopes of the tangent lines to your node, you need to solve some polynomial equations. Since is not algebraically closed, you may be unable to solve these equations in . That’s what happens in case 4). But you can always solve these equations in some algebraic extension of : that is, some bigger field where .
Next time I want to give some examples of reducing elliptic curves mod . I want to illustrate some things that can happen, and how the different cases above affect patterns in the count of points not just over but also over where is any power of .
I also want to say what this ‘additive’ and ‘multiplicative’ jargon is all about!

Another form of the definition
Let and let denote the discriminant. The L-function of is (See (10.9) of https://doi.org/10.2307/j.ctv346st5.16.) This seems pretty clean to me given the fact that it’s (ugh) number theory. Taniyama-Shimura boils down to the existence of a newform of weight two for with coefficients equal to for . Also pretty clean IMO considering.