Pythagorean Triples and the Projective Line
Posted by John Baez
Pythagorean triples like may seem merely cute, but they’re connected to some important ideas in algebra. To start seeing this, note that rescaling any Pythagorean triple gives a point with rational coordinates on the unit circle:
Conversely any point with rational coordinates on the unit circle can be scaled up to get a Pythagorean triple.
Now, if you’re a topologist or differential geometer you’ll know the unit circle is isomorphic to the real projective line as a topological space, and as a smooth manifold. You may even know they’re isomorphic as real algebraic varieties. But you may never have wondered whether the points with rational coordinates on the unit circle form a variety isomorphic to the rational projective line .
It’s true! And since is plus a point at infinity, this means there’s a way to turn rational numbers into Pythagorean triples. Working this out explicitly, this gives a nice explicit way to get our hands on all Pythagorean triples. And as a side-benefit, we see that points with rational coordinates are dense in the unit circle.
The basic idea is simple, but there’s a bit of suspense involved, and thus a bit to be learned.
First we set up an explicit isomorphism between and the unit circle . To do this, we think of as the axis in the plane together with a point at infinity. Then we map each point on the axis to a point on the unit circle by drawing a straight line through that point and the ‘north pole’ and seeing where it hits the circle:
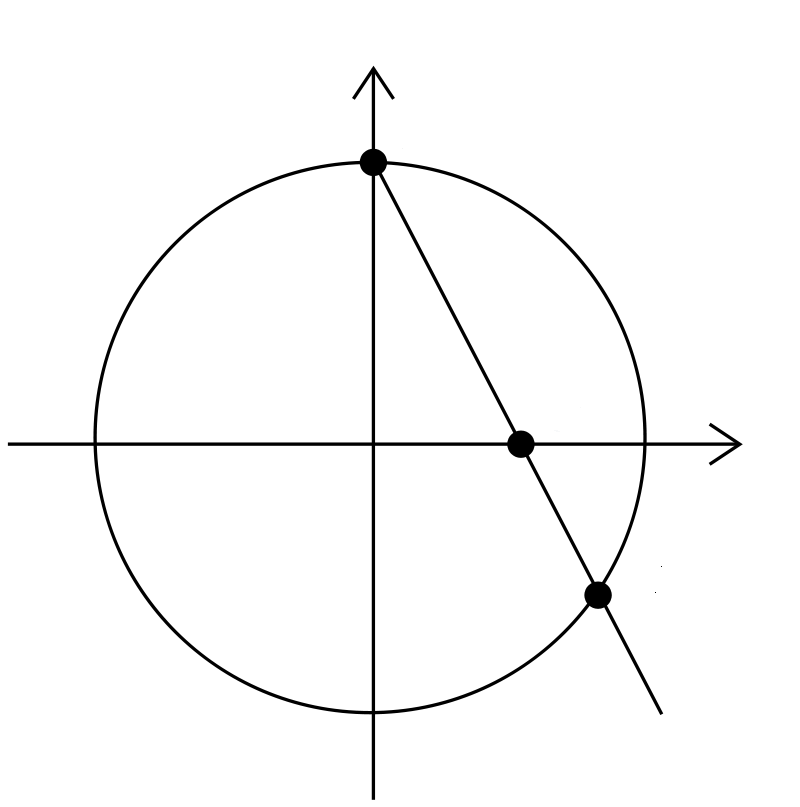
This extends to a bijection . Then we can restrict this to an isomorphism between and what I’ll call the rational unit circle
But there’s something to check here! Why does map rational numbers to points on with rational coordinates?
For this we need to think about . The line through the north pole and a point on the axis is given by
since this equation gives when and when . This line goes through some point on the unit circle. To figure out this point , notice it obeys the equation for the line and also
So plop the equation for the line into the equation for the circle and get
Now things get sort of interesting. It’s easy to solve this using the quadratic formula, but it’s not instantly obvious the solution will be rational when is rational! We could work it out and see, but a general principle saves us from this demeaning labor:
Lemma. If is a quadratic with coefficients in some field , and this quadratic has one root in , then the quadratic factors as in this field .
Our equation has rational coefficients when is rational, and we know it has one rational solution, namely , since the north pole lies both on the line and the circle. So the lemma says the other solution, the one we care about, must also be rational!
In short: whenever is rational so is , and then is as well, so is a point on the rational unit circle.
Since lines from the north pole to rational points on the axis hit the unit circle in a dense set, it follows that the rational unit circle is dense in the unit circle. And these correspond precisely to Pythagorean triples mod rescaling by integers. So we get all the Pythagorean triples this way, and a lot of them.
That makes it more interesting to see an explicit formula for . I joked that this would require “demeaning labor”. It’s just some algebra, but it’s a bit annoying. The main step is to solve the quadratic equation
or in other words
We could solve this using the quadratic formula—but that makes it seem a bit miraculous that in addition to the root , the root we care about will also be rational. It’s actually more fun to solve this equation using this proof of the Lemma:
Lemma. If is a quadratic with coefficients in some field , and this quadratic has one root in , then the quadratic factors as for some .
Proof. There’s a general abstract nonsense way to prove this, but it’s even quicker to show it directly and get a formula for . The quadratic must factor in the algebraic closure of , so
for . Thus
which lets us solve for one root if we know the other:
If the coefficients are in and the root is in , it follows that the root is also in . ∎
Since our quadratic
has one rational root , we see that the other root must be
That’s the root we want, so
See, this was more fun than using the quadratic formula and discovering that “miraculously” the answer is rational despite the square root! Simplifying a bit we get
which is much more cute. Then we get
Simplifying this we again get something much more cute:
So, our map from the rational projective line to the rational circle is
You can see this formula on Wikipedia, but I find the journey much more interesting than the destination… and we’re not even done with the journey.
But before we go on, we should at least take a moment to childishly flex our muscles. Take any rational number, like , and pop it into our formula for . We get
This means that
Rescaling, we get a Pythagorean triple:
Nice!
Further adventures
The unit circle is an example of a ‘conic’. Other examples include ellipses, hyperbolas and parabolas. Conics can be studied over any field , but it’s easiest to study them as projective varieties rather than affine varieties. To do that we take a quadratic form in 3 variables, see where it vanishes, and then ‘projectivize’: mod out by rescaling to get a subvariety of the projective plane. For example we get our friend the unit circle by projectivizing the real solutions of
and the same idea works for the rational unit circle if we use rational solutions.
Working projectively, we include ‘points at infinity’ which make our conics better behaved. The ordinary real hyperbola is obviously not isomorphic to , but when we work projectively it gets two points at infinity that fix this problem: you can sail out along one branch of the hyperbola to a point at infinity, sail back in along another branch, go out along that branch to another point at infinity, and then sail back to where you started. It’s really a circle viewed in a funny way!
I got interested in this stuff while writing about elliptic curves over finite fields. I suddenly realized I didn’t even understand conics over finite fields! This is like writing about cubic equations when you don’t even understand the quadratic equation. So I started learning about conics.
Among other things, I re-read Chapter 1 of Gille and Szamuely’s nice book Central Simple Algebras and Galois Cohomology, which explains the correspondence between projective conics over an arbitrary field and ‘quaternion algebras’ over that field, which are central simple algebras of dimension 4. I believe this should clarify the relation between Pythagorean triples and the algebra of integer matrices lurking behind Trautman’s work on Pythagorean spinors and the modular group. At least the algebra of rational matrices is a quaternion algebra over . But there seems to be something more going on here: some extension of the correspondence between conics and quaternion algebras over fields to certain more general commutative rings, including but also maybe all integral domains or something.
Why are Gille and Szamuely talking about conics and quaternion algebras? Because the correspondence between these led people to the more general correspondence between central simple algebras over a field and Severi–Brauer varieties over that field, which are varieties that become isomorphic to projective space when we pass to the algebraic closure . Attempting to classify these things led folks like Brauer, Hasse and Noether to invent what we’d now Galois cohomology, leading inexorably to modern homological algebra and descent theory. A great historical account is here:
- Peter Roquette, The Brauer–Hasse–Noether theorem in historical perspective.
I learned a lot of algebra from this paper; it’s a good supplement to Gille and Szamuely’s book.
But I digress. Gille and Szamuely write:
It is a well-known fact from algebraic geometry that a smooth projective conic defined over a field is isomorphic to the projective line over if and only if it has a -rational point. The isomorphism is given by taking the line joining a point of the conic to some fixed -rational point and then taking the intersection of this line with embedded as, say, some coordinate axis in .
As far as I can tell, a ‘-rational point’ is just a point defined over the field (rather than some algebraic extension). So they’re saying a smooth projective conic over a field that has any points in this simple sense must be isomorphic to the projective line . And their sketched proof of this generalizes the argument I presented above for . Discussing this over on the Category Theory Community Server, I got some help from people like Morgan Rogers, who pointed out the lemma used above. This lemma should guarantee that if a line in intersects a conic transversally at one point it intersects it in some other point.

Re: Pythagorean Triples and the Projective Line
When computing the intersection points, I find it easier to use the parametric form of the line, so , the reason being that is one intersection point. Explicitly so the other point of intersection is when , yielding of course the point