Line Bundles on Complex Tori (Part 3)
Posted by John Baez
You thought this series was dead. But it was only dormant!
In Part 1, I explained how the classification of holomorphic line bundles on a complex torus breaks into two parts:
the ‘discrete part’: their underlying topological line bundles are classified by elements of a free abelian group called the Néron–Severi group .
the ‘continuous part’: the holomorphic line bundles with a given underlying topological line bundle are classified by elements of a complex torus called the Jacobian .
In Part 2, I explained duality for complex tori, which is a spinoff of duality for complex vector spaces. I used this to give several concrete descriptions of the Néron–Severi group .
But the fun for me lies in the examples. Today let’s actually compute a Néron–Severi group and begin seeing how it leads to this remarkable picture by Roice Nelson:
This is joint work with James Dolan.
The most interesting complex tori are the complex abelian varieties. These are not just complex manifolds: they’re projective varieties, so the ideas of algebraic geometry apply! To be precise, a complex abelian variety is an abelian group object in the category of smooth complex projective varieties.
If you want to learn the general theory, I recommend this:
- Christina Birkenhake and Herbert Lange, Complex Abelian Varieties, Springer, Berlin, 2013.
It’s given me more pleasure than any book I’ve read for a long time. One reason is that it ties the theory nicely to ideas from physics, like the Heisenberg group and — without coming out and saying so — geometric quantization. Another is that abelian varieties are a charming, safe playground for beginners in algebraic geometry. You can easily compute things, classify things, and so on. It really amounts to linear algebra where all your vector spaces have lattices in them.
But instead of talking about general theorems, I’d like to look at an interesting example.
Every 1-dimensional complex torus can be made into an abelian variety: 1-dimensional abelian varieties are called elliptic curves, and everyone loves them. In higher dimensions the story is completely different: most complex tori can’t be made into abelian varieties! So, a lot of interesting phenomena are first seen in dimension 2. 2-dimensional abelian varieties are called complex abelian surfaces.
Here’s a cheap way to get our hands on an abelian surface: take the product of two elliptic curves. It’s tempting to use one of the two most symmetrical elliptic curves:
- The Gaussian curve , where
is called the ring of Gaussian integers because it’s the ring of algebraic integers in the field .
- The Eisenstein curve , where
and is the cube root of unity . is called the ring of Eisenstein integers because its the ring of algebraic integers in the field .
The Gaussian integers form a square lattice:
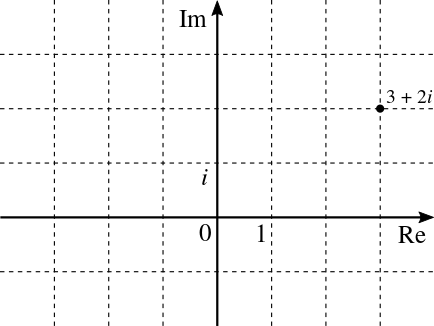
while the Eisenstein integers form an equilateral triangular lattice:
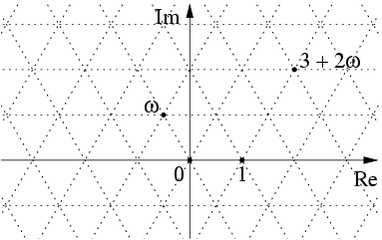
There are no other lattices in the plane as symmetrical as these, though there are interesting runners-up coming from algebraic integers in other fields .
Since the Eisenstein curve has 6-fold symmetry while the Gaussian curve has only 4-fold symmetry, let’s go all out and form an abelian surface by taking a product of two copies of the Eistenstein curve! I’ll call it the Eisenstein surface:
What are the symmetries of this? Like any complex torus, it acts on itself by translations. These are incredibly important, but they don’t preserve the group structure because they move the origin around. When we talk about morphisms of abelian varieties, we usually mean maps of varieties that also preserve the group structure. So what are the automorphisms of as an abelian variety?
Well, actually it’s nice to think about endomorphisms of as an abelian variety. Suppose is any matrix of Eisenstein integers. Then acts on in a linear way, by matrix multiplication. It obviously maps the lattice to itself. So it defines an endomorphism of . In other words, it gives an endomorphism of the Eisenstein surface as an abelian variety!
It’s not hard to see that these are all we get. So
Note that these endomorphisms form a ring: not only can you multiply them (i.e. compose them), you can also add them pointwise. Indeed any abelian variety has a ring of endomorphisms for the same reason, and these rings are very important in the overall theory.
Among the endomorphisms are the automorphisms, and I believe the automorphism group of the Eisenstein surface is
This is an infinite group because it contains ‘shears’ like
Now, what about line bundles on the Eisenstein surface ? Let’s sketch how to figure out its Néron–Severi group . Remember, this is a coarse classification of holomorphic line bundles where two count as the same if they are topologically isomorphic. Thus we get a discrete classification, not a ‘moduli space’.
I described the Néron–Severi group in a bunch of ways in Part 2. Here’s the one we want now. If is a complex torus we can write
where is a finite-dimensional complex vector space and is a lattice in . The vector space has a dual , defined in the usual way, and the lattice also has a dual , defined in a different way:
Then we saw something I called Theorem :
Theorem . The Néron–Severi group consists of linear maps that map into and have .
The point here is that any linear map has an adjoint , so the map has an adjoint , but the double dual of is canonically isomorphic to itself, so with a nod and a wink we can write , so it makes sense to say .
You may be slightly dazed now — are you seeing stars? Luckily, all of this becomes less confusing in our actual example where and , since the standard inner product on lets us identify this vector space with its dual, and — check this out, this part is not quite trivial — that lets us identify the lattice with its dual!
So, the Neron–Severi group of the Eisenstein surface consists of complex matrices that map to itself and are self-adjoint!
But it’s even simpler than that, since complex matrices that map to itself are just matrices of Eisenstein integers. The set of these is our friend . But now we want the self-adjoint ones. I’ll denote the set of these by . Here the gothic stands for ‘hermitian’.
So we’ve figured out the Neron–Severi group of the Eisenstein surface. It consists of hermitian matrices of Eisenstein integers:
Now let’s try to visualize it.
The fun part
I’ll dig into this more next time, but let me state the marvelous facts now, just to whet your appetite. The space of all complex self-adjoint matrices, called , is famous in physics. It’s 4-dimensional — and it’s a nice way of thinking about Minkowski spacetime, our model of spacetime in special relativity.
Sitting inside Minkowski spacetime, we now see the lattice of self-adjoint matrices with Eisenstein number entries. It’s a very nice discretization of spacetime.
It’s a bit hard to visualize 4-dimensional things. So let’s look at self-adjoint matrices whose determinant is and whose trace is positive. These form a 3-dimensional hyperboloid in Minkowski spacetime, called hyperbolic space. And it’s no hyperbole to say that this a staggeringly beautiful alternative to 3-dimensional Euclidean space. It’s negatively curved, so lines that start out parallel get further and further apart in an exponential way as they march along. There’s a lot more room in hyperbolic space — a lot of room for fun.
What happens if we look at points in our lattice that happen to lie in hyperbolic space? I believe we get the centers of the hexagons in this picture:
And I believe the other features of this picture arise from other relationships between and hyperbolic space. There’s a lot to check here. Greg Egan has made a lot of progress, but I’ll talk about that next time.
One last thing. I showed you that elements of correspond to topological isomorphism classes of holomorphic line bundles on the Eisenstein surface. Then I showed you a cool picture of a subset of , namely the elements with determinant and trace . But what’s the importance of these? Am I focusing on them merely to get a charismatic picture in hyperbolic space?
No: it turns out that these elements correspond to something really nice: principal polarizations of the Eisenstein surface! These come from very best line bundles, in a certain precise sense.


Re: Line Bundles on Complex Tori (Part 3)
By the way, I believe the whole analysis so far also works for the Gaussian surface formed as the product of two copies of the Gaussian elliptic curve :
We have
and most excitingly
I think the points of with determinant 1 and trace > 0 lie at the centers of the squares here: