August 31, 2014
Uncountably Categorical Theories
Posted by John Baez
Right now I’d love to understand something a logician at Oxford tried to explain to me over lunch a while back. His name is Boris Zilber. He’s studying what he informally calls ‘logically perfect’ theories — that is, lists of axioms that almost completely determine the structure they’re trying to describe. He thinks that we could understand physics better if we thought harder about these logically perfect theories:
Boris Zilber, Perfect infinities and finite approximation.
Boris Zilber, On model theory, noncommutative geometry and physics.
His ways of thinking, rooted in model theory, are quite different from anything I’m used to.
August 25, 2014
Why It Matters
Posted by Tom Leinster
One interesting feature of the Category Theory conference in Cambridge last month was that lots of the other participants started conversations with me about the whole-population, suspicionless surveillance that several governments are now operating. All but one were enthusiastically supportive of the work I’ve been doing to try to get the mathematical community to take responsibility for its part in this, and I appreciated that very much.
The remaining one was a friend who wasn’t unsupportive, but said to me something like “I think I probably agree with you, but I’m not sure. I don’t see why it matters. Persuade me!”
Here’s what I replied.
August 20, 2014
Holy Crap, Do You Know What A Compact Ring Is?
Posted by Tom Leinster
You know how sometimes someone tells you a theorem, and it’s obviously false, and you reach for one of the many easy counterexamples only to realize that it’s not a counterexample after all, then you reach for another one and another one and find that they fail too, and you begin to concede the possibility that the theorem might not actually be false after all, and you feel your world start to shift on its axis, and you think to yourself: “Why did no one tell me this before?”
That’s what happened to me today, when my PhD student Barry Devlin — who’s currently writing what promises to be a rather nice thesis on codensity monads and topological algebras — showed me this theorem:
Every compact Hausdorff ring is totally disconnected.
August 12, 2014
The Tenfold Way (Part 4)
Posted by John Baez
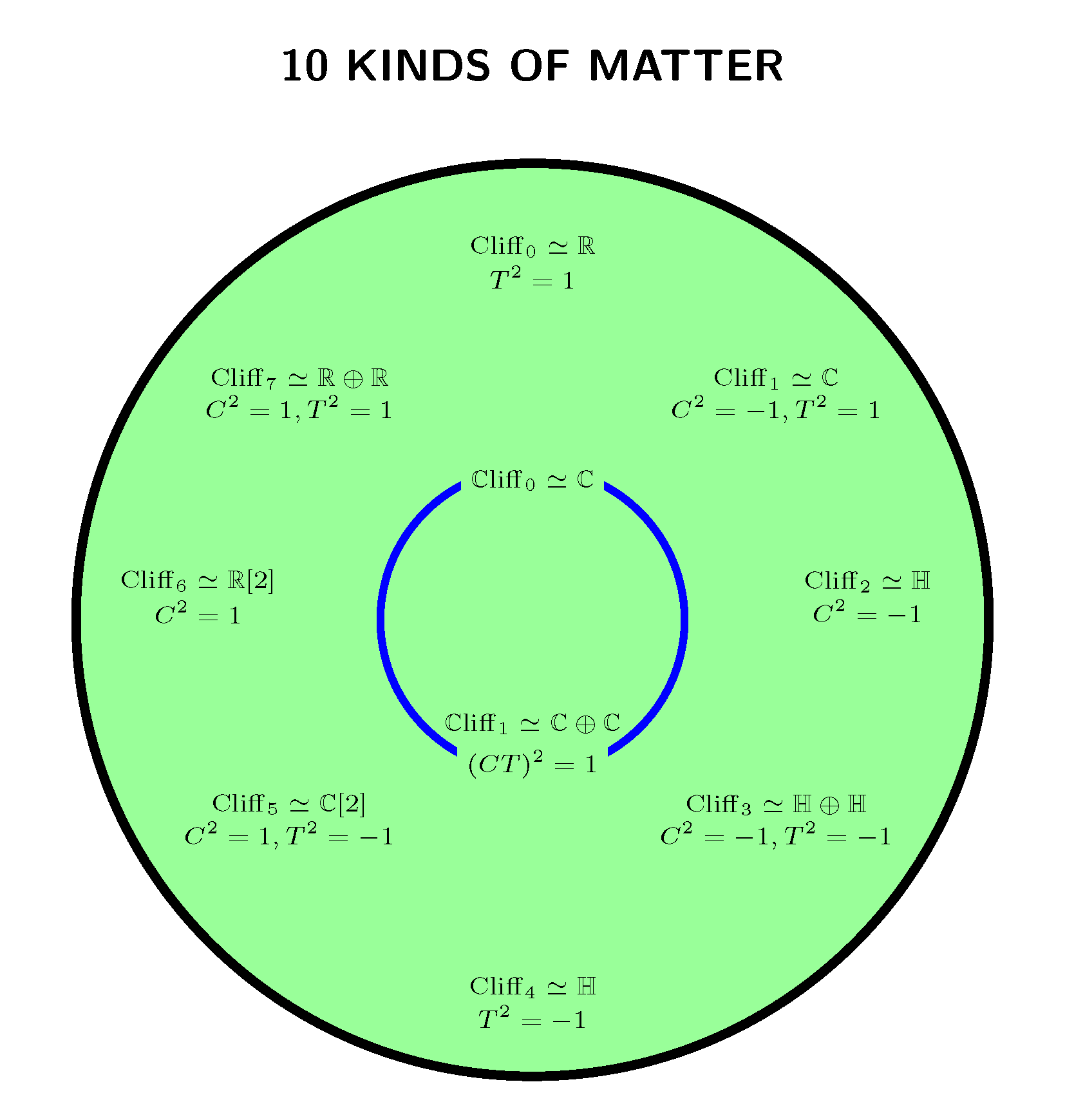
Back in 2005, Todd Trimble came out with a short paper on the super Brauer group and super division algebras, which I’d like to TeXify and reprint here.
In it, he gives extremely efficient proofs of several facts I alluded to last time. Namely:
• There are exactly 10 real division superalgebras.
• 8 of them have center , and these are Morita equivalent to the real Clifford algebras .
• 2 of them have center , and these are Morita equivalent to the complex Clifford algebras and .
• The real Clifford algebras obey
where means they’re Morita equivalent as superalgebras.
It easily follows from his calculations that also:
• The complex Clifford algebras obey
These facts lie at the heart of the ten-fold way. So, let’s see why they’re true!
August 7, 2014
The Tenfold Way (Part 3)
Posted by John Baez
My last article on the ten-fold way was a piece of research in progress — it only reached a nice final form in the comments. Since that made it rather hard to follow, let me try to present a more detailed and self-contained treatment here!
But if you’re in a hurry, you can click on this:
and get my poster for next week’s scientific advisory board meeting at the Centre for Quantum Technologies, in Singapore. That’s where I work in the summer, and this poster is supposed to be a terse introduction to the ten-fold way.
August 2, 2014
Wrestling with Tight Spans
Posted by Tom Leinster
I’ve been spending some time with Simon Willerton’s paper Tight spans, Isbell completions and semi-tropical modules. In particular, I’ve been trying to understand tight spans.
The tight span of a metric space is another metric space , in which naturally embeds. For instance, the tight span of a two-point space is a line segment containing the original two points as its endpoints. Similarly, the tight span of a three-point space is a space shaped like the letter Y, with the original three points at its tips. Because of examples like this, some people like to think of the tight span as a kind of abstract convex hull.
Simon’s paper puts the tight span construction into the context of a categorical construction, Isbell conjugacy. I now understand these things better than I did, but there’s still a lot I don’t get. Here goes.
 Posts with this logo use
Posts with this logo use