March 28, 2024
Why Mathematics is Boring
Posted by John Baez
I’m writing a short article with some thoughts on how to write math papers, with a provocative title. It’s due very soon, so if you have any thoughts about this draft I’d like to hear them soon!
March 23, 2024
Counting Points on Elliptic Curves (Part 3)
Posted by John Baez
In Part 1 of this little series I showed you Wikipedia’s current definition of the -function of an elliptic curve, and you were supposed to shudder in horror. In this definition the -function is a product over all primes . But what do we multiply in this product? There are 4 different cases, each with its own weird and unmotivated formula!
In Part 2 we studied the 4 cases. They correspond to 4 things that can happen when we look at our elliptic curve over the finite field : it can stay smooth, or it can become singular in 3 different ways. In each case we got a formula for number of points the resulting curve over the fields .
Now I’ll give a much better definition of the -function of an elliptic curve. Using our work from last time, I’ll show that it’s equivalent to the horrible definition on Wikipedia. And eventually I may get up the nerve to improve the Wikipedia definition. Then future generations will wonder what I was complaining about.
March 13, 2024
Counting Points on Elliptic Curves (Part 2)
Posted by John Baez
Last time I explained three ways that good curves can go bad. We start with an equation like
where is a cubic with integer coefficients. This may define a perfectly nice smooth curve over the complex numbers — called an ‘elliptic curve’ — and yet when we look at its solutions in finite fields, the resulting curves over those finite fields may fail to be smooth. And they can do it in three ways.
Let’s look at examples.
March 10, 2024
Counting Points on Elliptic Curves (Part 1)
Posted by John Baez
You’ve probably heard that there are a lot of deep conjectures about -functions. For example, there’s the Langlands program. And I guess the Riemann Hypothesis counts too, because the Riemann zeta function is the grand-daddy of all -functions. But there’s also a million-dollar prize for proving the Birch-Swinnerton–Dyer conjecture about -functions of elliptic curves. So if you want to learn about this stuff, you may try to learn the definition of an -function of an elliptic curve.
But in many expository accounts you’ll meet a big roadblock to understanding.
The -function of elliptic curve is often written as a product over primes. For most primes the factor in this product looks pretty unpleasant… but worse, for a certain finite set of ‘bad’ primes the factor looks completely different, in one of 3 different ways. Many authors don’t explain why the -function has this complicated appearance. Others say that tweaks must be made for bad primes to make sure the -function is a modular form, and leave it at that.
I don’t think it needs to be this way.
March 9, 2024
Semi-Simplicial Types, Part I: Motivation and History
Posted by Mike Shulman
(Jointly written by Astra Kolomatskaia and Mike Shulman)
This is part one of a three-part series of expository posts on our paper Displayed Type Theory and Semi-Simplicial Types. In this part, we motivate the problem of constructing SSTs and recap its history.
March 3, 2024
Modular Curves and Monstrous Moonshine
Posted by John Baez
Recently James Dolan and I have been playing around with modular curves — more specifically the curves and , which I’ll explain below. Monstrous Moonshine says that when is prime, the curve has genus zero iff divides the order of the Monster group, namely
Just for fun we’ve been looking at , among other cases. We used dessins d’enfant to draw a picture of , which seems to have genus , so for to have genus zero it seems we want the picture for to have a visible two-fold symmetry. After all, the torus is a two-fold branched cover of the sphere, as shown by Greg Egan here:
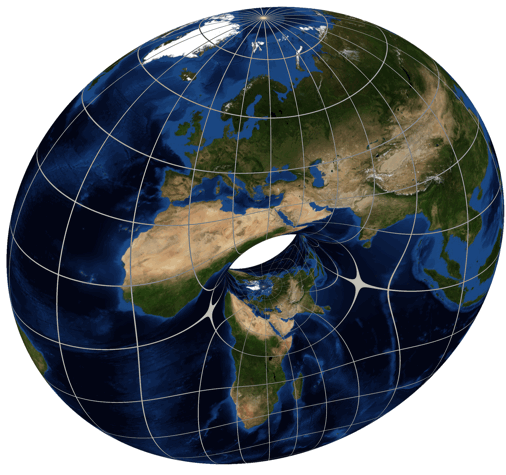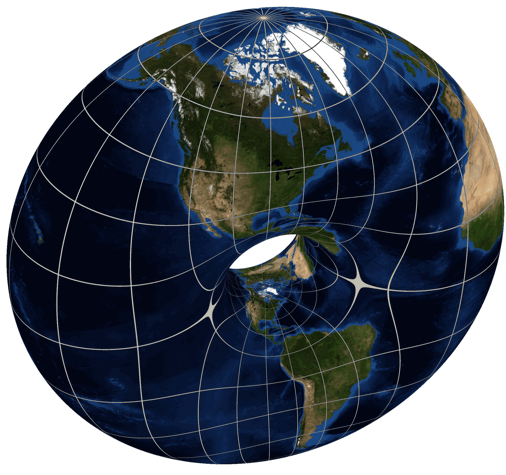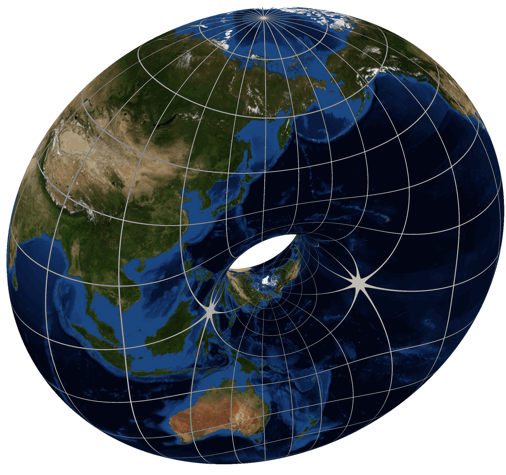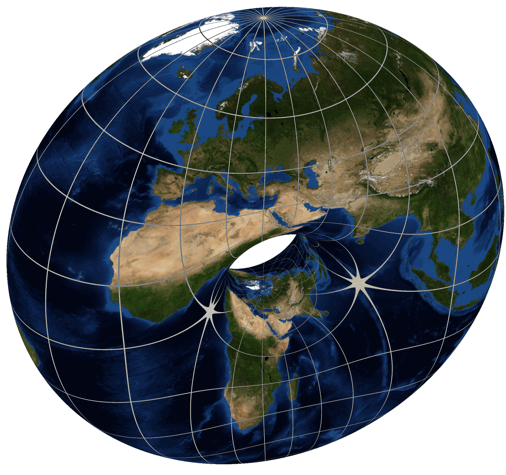
But we’re not seeing that two-fold symmetry. So maybe we’re making some mistake!
Maybe you can help us, or maybe you’d just like a quick explanation of what we’re messing around with.
 Posts with this logo use
Posts with this logo use 














