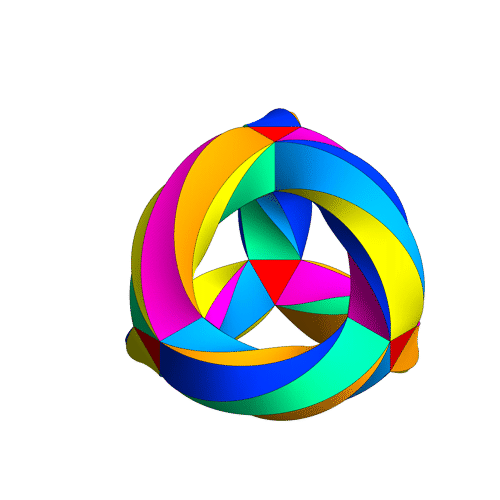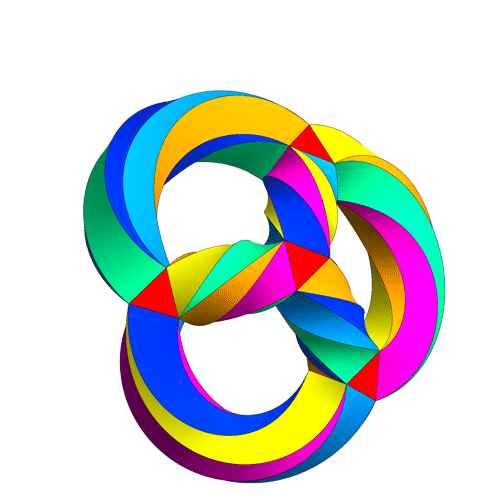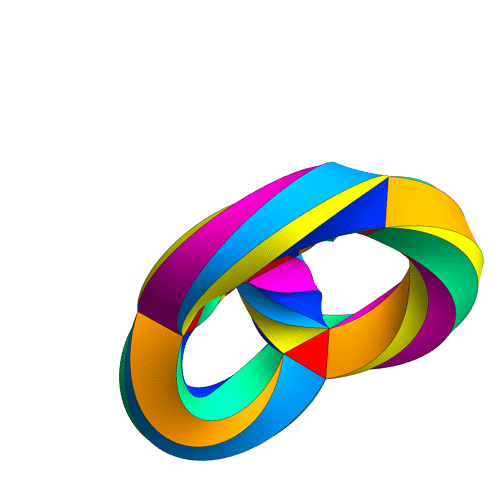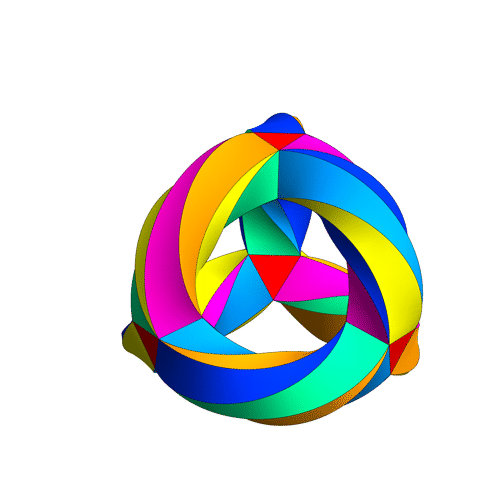Skip to the Main Content

Note:These pages make extensive use of the latest XHTML and CSS Standards. They ought to look great in any standards-compliant modern browser. Unfortunately, they will probably look horrible in older browsers, like Netscape 4.x and IE 4.x. Moreover, many posts use MathML, which is, currently only supported in Mozilla. My best suggestion (and you will thank me when surfing an ever-increasing number of sites on the web which have been crafted to use the new standards) is to upgrade to the latest version of your browser. If that's not possible, consider moving to the Standards-compliant and open-source Mozilla browser.

April 30, 2016

Relative Endomorphisms

Posted by Qiaochu Yuan

Let (M,⊗)(M, \otimes) be a monoidal category and let CC be a left module category over MM, with action map also denoted by ⊗\otimes. If m∈Mm \in M is a monoid and c∈Cc \in C is an object, then we can talk about an action of mm on cc: it’s just a map

α:m⊗c→c\alpha : m \otimes c \to c

satisfying the usual associativity and unit axioms. (The fact that all we need is an action of MM on CC to define an action of mm on cc is a cute instance of the microcosm principle.)

This is a very general definition of monoid acting on an object which includes, as special cases (at least if enough colimits exist),

  • actions of monoids in Set\text{Set} on objects in ordinary categories,
  • actions of monoids in Vect\text{Vect} (that is, algebras) on objects in Vect\text{Vect}-enriched categories,
  • actions of monads (letting M=End(C)M = \text{End}(C)), and
  • actions of operads (letting CC be a symmetric monoidal category and MM be the monoidal category of symmetric sequences under the composition product)

This definition can be used, among other things, to straightforwardly motivate the definition of a monad (as I did here): actions of a monoidal category MM on a category CC correspond to monoidal functors M→End(C)M \to \text{End}(C), so every action in the above sense is equivalent to an action of a monad, namely the image of the monoid mm under such a monoidal functor. In other words, monads on CC are the universal monoids which act on objects c∈Cc \in C in the above sense.

Corresponding to this notion of action is a notion of endomorphism object. Say that the relative endomorphism object End M(c)\text{End}_M(c), if it exists, is the universal monoid in MM acting on cc: that is, it’s a monoid acting on cc, and the action of any other monoid on cc uniquely factors through it.

Continue reading “Relative Endomorphisms” …
Posted at 1:40 AM UTC | Permalink | Followups (9)

April 23, 2016

Polygonal Decompositions of Surfaces

Posted by John Baez

If you tell me you’re going to take a compact smooth 2-dimensional manifold and subdivide it into polygons, I know what you mean. You mean something like this picture by Norton Starr:

or this picture by Greg Egan:

(Click on the images for details.) But what’s the usual term for this concept, and the precise definition? I’m writing a paper that uses this concept, and I don’t want to spend my time proving basic stuff. I want to just refer to something.

Continue reading “Polygonal Decompositions of Surfaces” …
Posted at 4:54 PM UTC | Permalink | Followups (14)

April 21, 2016

Type Theory and Philosophy at Kent

Posted by David Corfield

I haven’t been around here much lately, but I would like to announce this workshop I’m running on 9-10 June, Type Theory and Philosophy. Following some of the links there will show, I hope, the scope of what may be possible.

One link is to the latest draft of an article I’m writing, Expressing ‘The Structure of’ in Homotopy Type Theory, which has evolved a little over the year since I posted The Structure of A.

Posted at 2:05 PM UTC | Permalink | Post a Comment