March 31, 2021
Can We Understand the Standard Model Using Octonions?
Posted by John Baez
I gave two talks in Latham Boyle and Kirill Krasnov’s Perimeter Institute workshop Octonions and the Standard Model.
The first talk was on Monday April 5th at noon Eastern Time. The second was exactly one week later, on Monday April 12th at noon Eastern Time.
Here they are…
March 29, 2021
Native Type Theory (Part 3)
Posted by John Baez
guest post by Christian Williams
In Part 2 we described higher-order algebraic theories: categories with products and finite-order exponents, which present languages with (binding) operations, equations, and rewrites; from these we construct native type systems.
Now let’s use the wisdom of the Yoneda embedding!
March 21, 2021
Native Type Theory (Part 2)
Posted by John Baez
guest post by Christian Williams
We’re continuing the story of Native Type Theory.
In Part 1 we introduced the internal language of a topos. Now, we describe the kinds of categories from which we will construct native type systems, via the internal language of the presheaf topos .
March 18, 2021
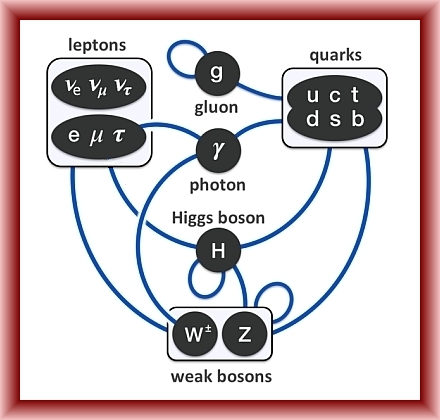
A Group Theory Problem
Posted by John Baez
Preparing a talk on octonions and the Standard Model, I’m struggling with a calculation in this paper:
- Michel Dubois-Violette and Ivan Todorov, Exceptional quantum geometry and particle physics II.
and I’d like your help. The essence of the problem is nothing about octonions, it’s about Lie groups — and pretty simple Lie groups too, like and . So, there’s a good chance you can help me out. I’ll explain it.
March 17, 2021
Can We Understand The Standard Model?
Posted by John Baez
I’m giving a talk in Latham Boyle and Kirill Krasnov’s Perimeter Institute workshop Octonions and the Standard Model on Monday April 5th at noon Eastern Time.
This talk will be a review of some facts about the Standard Model. Later I’ll give one that says more about the octonions.
Mathematics in the 21st Century
Posted by John Baez
I’m giving a talk in the Topos Institute Colloquium on Thursday March 25, 2021 at 18:00 UTC. I believe that’s 11:00 am Pacific Time. In any event, that’s when I plan to show up.
As usual for them, it will be broadcast live on Zoom and also on YouTube, where it will be recorded for posterity. Only Zoom lets you ask questions. The password for Zoom can be found on the Topos Institute Colloquium website.
March 14, 2021
Emerging Researchers in Category Theory
Posted by John Baez
Eugenia Cheng is an expert on giving clear, fun math talks.
Now you can take a free class from her on how to give clear, fun math talks!
You need to be a grad student in category theory, and priority will be given to those who aren’t at fancy schools, etc.
Her course is called the Emerging Researchers in Category Theory Virtual Seminar, or Em-Cats for short. You — or some student you know! — can apply for it here:
The first round of applications is due April 30th. It looks pretty cool, and knowing Eugenia, you’ll get a lot of help on giving talks.
March 8, 2021
Parametric adjoints = multi-adjoints
Posted by Mike Shulman
Here are two “weakenings” of the notion of adjoint functor:
If has a terminal object , a functor is a parametric right adjoint if the induced functor is a right adjoint.
A functor has a left multi-adjoint if for each there is a (small) family of morphisms such that for any morphism , there is a unique pair of an index and a morphism such that .
I just noticed that these two definitions are almost exactly the same! Specifically, if has a terminal object and is locally small, then a functor is a parametric right adjoint if and only if it has a left multi-adjoint.
March 2, 2021
Postdoctoral Position in Higher Category Theory at Johns Hopkins University
Posted by Emily Riehl
The Department of Mathematics at Johns Hopkins University solicits applications for one two-year postdoctoral fellowship beginning Summer 2021 (with some flexibility in the start and end dates). The position is funded by the Army Research Office (ARO) through the Multidisciplinary University Research Initiative (MURI) program. This position is open to anyone who is able to obtain a visa to come and work in the US, but it is necessary to be physically in the US to receive funding from this grant. (Johns Hopkins will sponsor and pay for a visa application, if required.)
The -Category Café has recently hosted a lively discussion on the ethics of military funded mathematics and US military funding in particular. This is the first time I’ve collaborated on a military funded grant, so I have limited experience in this area. But every year, I’m heartbroken to disappoint the dozens of highly-qualified postdoctoral applicants I come in contact with. My department also offers university-funded postdoctoral positions (though one could argue that military funding provides some support for all employees at Johns Hopkins) but at some point I calculated that it would be “my turn” to make an offer to my first choice candidate exactly once a decade, and I wanted to try to find a way to hire others in the meanwhile.
Funding of the nLab
Posted by David Corfield
The nLab was born out of conversations at the Café back in 2008. Over the past 12 years it has grown as a wiki to over 15000 pages.
For many years it was funded personally by Urs Schreiber, until in the last few years when it relied on a fund kindly provided by Steve Awodey.
But now we have new arrangements in place, and are looking to its users to help fund the nLab:
In 2021, the nLab will move to the cloud. To fund the running of the nLab in the cloud, we have decided to rely upon funding by donations. In the autumn of 2020, at the kind initiative of Brendan Fong, the nLab decided to collaborate with the Topos Institute for the practical side of this: the Topos Institute is legally able to handle donations, and the financing of the nLab will be handled by the Topos Institute. The Topos Institute owns the cloud account in which the nLab will be run.
Please do consider making a donation here.
March 1, 2021
Theoretical Physics in the 21st Century
Posted by John Baez
I’m giving a talk at the Zürich Theoretical Physics Colloquium next Monday, for Sustainability Week 2021. I’m excited to get a chance to speak both about the future of theoretical physics and the climate crisis. You can attend if you want.
 Posts with this logo use
Posts with this logo use