May 28, 2010
The Quantum Whisky Club
Posted by John Baez
I’m live blogging from the Quantum Whisky Club. We’re in a dimly-lit office in the Computing Lab at Oxford University, listening to a rap song about Pythagoras composed by Richard Garner, who is here along with a bunch of other folks who’ll be attending the Quantum Physics and Logic workshop.
Like who?
May 27, 2010
nLab Digest
Posted by David Corfield
I wanted to give people an idea of what has been going on in recent weeks at the very active nLab and associated personal wikis, so I asked members to describe some of the important contributions of late. Before I relay these, remember that anyone is welcome to participate in this great collaborative project, and also to join in discussions at nForum.
Let’s hear first from Urs Schreiber.
May 26, 2010
Nonabelian Cohomology in Three (∞,1)-Toposes
Posted by Urs Schreiber
For a topological space and an ∞-groupoid, the standard way to define the nonabelian cohomology of with coefficients in is to define it as the intrinsic cohomology as seen in ∞Grpd Top:
where is the geometric realization of and the fundamental ∞-groupoid of .
But both and here naturally can be regarded, in several ways, as objects of (∞,1)-sheaf (∞,1)-toposes over nontrivial (∞,1)-sites . The intrinsic cohomology of such is a nonabelian sheaf cohomology.
The following discusses two such choices for such that the corresponding nonabelian sheaf cohomology coincides with (for paracompact ).
May 18, 2010
Squeezing Higher Categories out of Lower Categories
Posted by Mike Shulman
For a long time, homotopy theory involved the study of homotopy categories. More recently, people have started preferring to use -categories, since homotopy categories lose a lot of structure. But it’s worth remembering that homotopy categories do still contain a lot of information, and moreover they encapsulate it all in terms of the familar and easy-to-handle notions of 1-category theory. Want to know if two spaces are (weak) homotopy equivalent? Check whether they’re isomorphic in the homotopy category. Want to know the homotopy groups of a (pointed connected) space? Look at maps out of spheres in the homotopy category. Want a representing object for cohomology theory? Apply Brown’s representability theorem in the homotopy category. Want to know the homotopy type of a mapping space? You’re in luck: the homotopy category is closed symmetric monoidal.
Today I want to talk about ways we can use lower-categorical “homotopy categories” to squeeze even more information out of a higher category, without ever having to construct and work with that higher category directly (thereby potentially avoiding a lot of combinatorial complexity). In fact, in good situations, we can actually squeeze out all the information in this way! (At least for a suitable definition of “all.”)
May 15, 2010
This Week’s Finds in Mathematical Physics (Week 298)
Posted by John Baez
In "week298" of This Week’s Finds, learn about finite subgroups of the unit quaternions, like the binary icosahedral group:
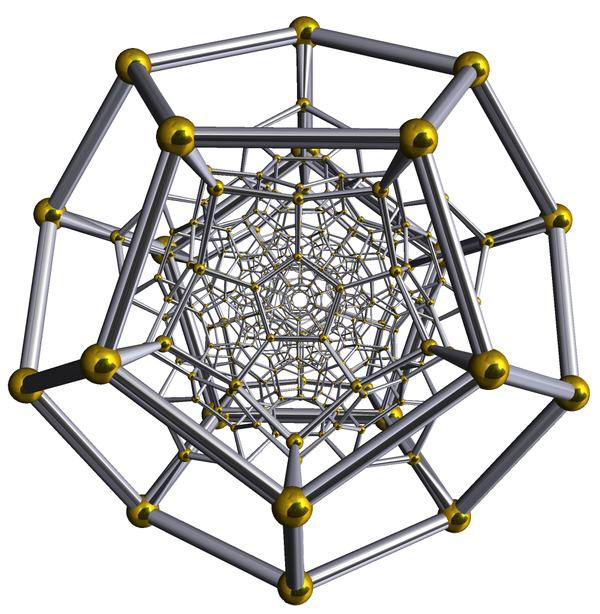
Then meet the finite subloops of the unit octonions. Get a tiny taste of how division algebras can be used to build Lie n-superalgebras that govern superstring and supermembrane theories. And meet Duff and Ferrara’s ideas connecting exceptional groups to Cayley’s hyperdeterminants and entanglement in quantum information theory.
May 10, 2010
Quinn on Higher-Dimensional Algebra
Posted by David Corfield
Frank Quinn kindly wrote to me to point out an essay he is working on – The Nature of Contemporary Core Mathematics (version 0.92). Quinn will be known to many readers here as a mathematician who has worked in low-dimensional topology, and as one of the authors, with Arthur Jaffe, of “Theoretical mathematics”: Toward a cultural synthesis of mathematics and theoretical physics.
I crop up in the tenth section of the article, which is devoted to a discussion of “a few other accounts of mathematics”, including those of Barry Mazur, Jonathan Borwein, Keith Devlin, Michael Stöltzner, and William Thurston.
One objective is to try to understand why such accounts are so diverse and mostly – it seems to me – irrelevant when they all ostensibly concern the same thing. The mainstream philosophy of mathematics literature seems particularly irrelevant, and the reasons shallow and uninteresting, so only two are considered here. Essays by people with significant mathematical background often have useful insights, and when they seem off-base to me the reasons are revealing. The essay by Mazur is not off-base. (p. 53)
I take it that “irrelevant” is being taken relative to Quinn’s interest in characterising ‘Core Mathematics’.
This Week’s Finds in Mathematical Physics (Week 297)
Posted by John Baez
In week297 of This Week’s Finds, see some knot sculptures by Karel Vreeburg:
Read about special relativity in finance. Learn about lazulinos. Admire some peculiar infinite sums. Ponder a marvelous property of the number 12. Then: learn about the role of Dirichlet forms in electrical circuit theory!
May 8, 2010
The Scottish Category Theory Seminar
Posted by Tom Leinster
The Scottish Category Theory Seminar is a newish series of occasional afternoon meetings, at locations roaming around the country (though there’ll probably never be any on highland mountaintops or remote misty lochs…). I’m very pleased to announce the second meeting of the seminar, in Edinburgh on Friday 21 May.
We’ve worked hard to get a good mixture of mathematicians on the one hand, and theoretical computer scientists on the other. Two of the speakers, Antony Maciocia and Peter Kropholler, are mathematicians — Maciocia is in algebraic geometry, and Kropholler at the intersection of group theory and topology. The other two, Dirk Pattinson and Thorsten Altenkirch, are in theoretical computer science — though their talks should definitely be interesting to mathematicians.
All the speakers have been firmly requested to make their talks broadly accessible to what we hope will be a very mixed audience. So I’m looking forward to an excellent afternoon.
May 7, 2010
Back in Business
Posted by David Corfield
After a coolant leak knocked out the server which supports the Café, Golem IV rises from the ashes, allowing us all to get back to business. Our thanks go to Jacques Distler for his sterling effort.
[Update: I think comments aren’t working yet.]
[Update 2: Now they are.]
 Posts with this logo use
Posts with this logo use 















