June 26, 2023
Grothendieck–Galois–Brauer Theory (Part 1)
Posted by John Baez
I’m slowly cooking up a big stew of ideas connecting Grothendieck’s Galois theory to the Brauer 3-group, the tenfold way, the foundations of quantum physics and more. The stew is not ready yet, but I’d like you to take a taste.
June 24, 2023
Compositional System Dynamics for Public Health
Posted by John Baez
The Topos Institute has a colloquium every week. This time it’s by my old grad school pal Nate Osgood. He’s a computer scientist, he helped lead Canada’s COVID modeling effort…
… and he is now spear-heading a project to develop software that uses ideas from category theory to make it easier to create models of epidemic disease!
I am completely biased, since I’m involved in this — but I am really excited about how category theory, computer science and epidemiology are meeting in this project and yielding practical tools for public health.
His talk is Thursday June 29, 10:00-11:00 Pacific Time. To watch it either live or recorded go here.
It should be fun, because I believe he and his grad student Xiaoyan Li will attempt to assemble a disease model in real time using our software. Read on for more details.
June 23, 2023
ACT 2023 — Registration
Posted by John Baez
6th Annual International Conference on Applied Category Theory (ACT2023)
July 31 - August 4, 2023
Due to generous sponsorship from NIST and UFL, registration is completely free! Please register here:
https://www.eventbrite.com/e/applied-category-theory-2023-registration-643212404617
If you plan to attend virtually, you will need to register before July 14th to receive a Zoom link.
June 19, 2023
Research Fellowships in Representation Theory and/or Low Dimensional Topology at Leeds
Posted by Simon Willerton
A group at Leeds are looking for one or two Postdoctoral Research Fellows to work on the EPSRC Programme Grant: Combinatorial Representation Theory: Discovering the Interfaces of Algebra with Geometry and Topology.
The project is led by the six Investigators: Professor Karin Baur, principal investigator, together with co-investigators Professor Eleonore Faber, Dr Joao Faria Martins, Professor Bethany Marsh, Professor Paul Martin and Dr Alison Parker.
For details please see https://jobs.leeds.ac.uk/Vacancy.aspx?ref=EPSMA1084.
June 14, 2023
The Wedderburn–Artin Theorem
Posted by John Baez
Now that I finally understand the proof of the Wedderburn–Artin Theorem, I want to do what any good category theorist would do: formulate it more generally and abstractly, so nobody can understand me and I look like a genius everybody can see how simple it actually is.
June 11, 2023
Brauer’s Lemma
Posted by John Baez
The Wedderburn–Artin Theorem has always been one of my friends in ring theory, not because I understand it well, but because it reduces a potentially scary general situation to one that fits pretty nicely inside my mathematical physics brain. One proof of it uses a cute result called ‘Brauer’s Lemma’.
June 6, 2023
Commutative Separable Algebras III
Posted by John Baez
I wrote two blog articles on this theme back in 2010:
Now for rather different reasons I’m returning to it.
A separable algebra over a commutative ring is an algebra that’s projective as -module. That may sound dry, but you can see three other equivalent definitions here. For example, a separable algebra is an algebra that can be given a comultiplication obeying the Frobenius laws:
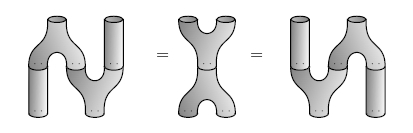
and the special law:
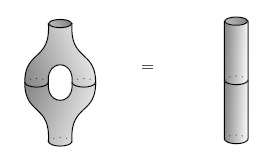
Lately I’ve been trying to understand Azumaya algebras, which are separable algebras over whose center is just . The interesting Azumaya algebras are of course the noncommutative ones, since the only commutative one is itself.
But commutative separable algebras are also interesting. They are important in Grothendieck’s approach to Galois theory. So, I want to understand them better, to better understand how Azumaya algebras are connected to Galois theory.
So, back to commutative separable algebras! And this time we’ll see how they show up in the Fundamental Theorem of Grothendieck Galois Theory!
June 2, 2023
Seminar on Applied Category Theory
Posted by David Corfield
I’m hosting a small symposium next Tuesday, 6 June, on Applied Category Theory, featuring our very own John Baez. Here’s the announcement.
The language of Category Theory has been under development since the 1940s and continues to evolve to this day. It was originally created as a formal language to capture common mathematical structures and inference methods across various branches of mathematics, and later found application outside of mathematics. By introducing arrows to mediate between objects, the language is designed to represent anything that can be perceived as a process - including processes of inference and physical processes.
The first applications of Category Theory outside of mathematics and logic were to physics and to computer science. There was also an early application in biology by Robert Rosen.
But over the past decade we have seen researchers under the banner of Applied Category Theory take on a variety of novel subjects, addressing topics which include:
causality, probabilistic reasoning, statistics, learning theory, deep neural networks, dynamical systems, information theory, database theory, natural language processing, cognition, consciousness, systems biology, genomics, epidemiology, chemical reaction networks, neuroscience, complex networks, game theory, robotics, and quantum computing.
In this hybrid seminar at the Centre for Reasoning, University of Kent, we will be hearing online from two leading practitioners. All are welcome to attend.
Location
In person: KS23, Keynes College, University of Kent, Canterbury
Online: MS Teams link
Schedule
UK time (UTC +1), Tuesday 6 June
15.30-15.50 David Corfield (Kent), Introduction: Applied Category Theory from a Philosophical Point of View
15.50-16.50 Toby St Clere Smithe (Topos Institute, Oxford), Understanding the Bayesian Brain with Categorical Cybernetics
17.00-18.00 John Baez (UC Riverside), Applied Category Theory
 Posts with this logo use
Posts with this logo use 














