July 31, 2017
A Compositional Framework for Reaction Networks
Posted by John Baez
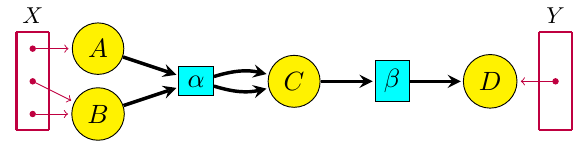
For a long time Blake Pollard and I have been working on ‘open’ chemical reaction networks: that is, networks of chemical reactions where some chemicals can flow in from an outside source, or flow out. The picture to keep in mind is something like this:
where the yellow circles are different kinds of chemicals and the aqua boxes are different reactions. The purple dots in the sets X and Y are ‘inputs’ and ‘outputs’, where certain kinds of chemicals can flow in or out.
Our paper on this stuff just got accepted, and it should appear soon:
- John Baez and Blake Pollard, A compositional framework for reaction networks, to appear in Reviews in Mathematical Physics.
But thanks to the arXiv, you don’t have to wait: beat the rush, click and download now!
Or at least read the rest of this blog post….
July 19, 2017
What is the Comprehension Construction?
Posted by Emily Riehl
Dominic Verity and I have just posted a paper on the arXiv entitled “The comprehension construction.” This post is meant to explain what we mean by the name.
The comprehension construction is somehow analogous to both the straightening and the unstraightening constructions introduced by Lurie in his development of the theory of quasi-categories. Most people use the term -categories as a rough synonym for quasi-categories, but we reserve this term for something more general: the objects in any -cosmos. There is an -cosmos whose objects are quasi-categories and another whose objects are complete Segal spaces. But there are also more exotic -cosmoi whose objects model -categories or fibered -categories, and our comprehension construction applies to any of these contexts.
The input to the comprehension construction is any cocartesian fibration between -categories together with a third -category . The output is then a particular homotopy coherent diagram that we refer to as the comprehension functor. In the case , the comprehension functor defines a “straightening” of the cocartesian fibration. In the case where the cocartesian fibration is the universal one over the quasi-category of small -categories, the comprehension functor converts a homotopy coherent diagram of shape into its “unstraightening,” a cocartesian fibration over .
The fact that the comprehension construction can be applied in any -cosmos has an immediate benefit. The codomain projection functor associated to an -category defines a cocartesian fibration in the slice -cosmos over , in which case the comprehension functor specializes to define the Yoneda embedding.
July 14, 2017
Laws of Mathematics “Commendable”
Posted by Tom Leinster
Australia’s Prime Minister Malcolm Turnbull, today:
The laws of mathematics are very commendable, but the only law that applies in Australia is the law of Australia.
The context: Turnbull wants Australia to undermine encryption by compelling backdoors by law. The argument is that governments should have the right to read all their citizens’ communications.
Technologists have explained over and over again why this won’t work, but politicians like Turnbull know better. The recent, enormous, Petya and WannaCry malware attacks (hitting British hospitals, for instance) show what can happen when intelligence agencies such as the NSA treat vulnerabilities in software as opportunities to be exploited rather than problems to be fixed.
Thanks to David Roberts for sending me the link.
July 8, 2017
A Bicategory of Decorated Cospans
Posted by John Baez
My students are trying to piece together general theory of networks, inspired by many examples. A good general theory should clarify and unify these examples. What some people call network theory, I’d just call ‘applied graph invariant theory’: they come up with a way to calculate numbers from graphs, they calculate these numbers for graphs that show up in nature, and then they try to draw conclusions about this. That’s fine as far as it goes, but there’s a lot more to network theory!
July 2, 2017
The Geometric McKay Correspondence (Part 2)
Posted by John Baez
Last time I sketched how the Dynkin diagram arises from the icosahedron. This time I’m fill in some details. I won’t fill in all the details, because I don’t know how! Working them out is the goal of this series, and I’d like to enlist your help.
As Kennedy said: ask not what your n-Café can do for you. Ask what you can do for your n-Café!
 Posts with this logo use
Posts with this logo use