December 29, 2020
Azat Miftakhov
Posted by John Baez
Azat Miftakhov is a finishing graduate student in Mathematics at Moscow State University, and is a political activist. In February 2019 he was arrested and charged with terrorist activity and the production of explosives. These charges were quickly dropped, but he is nevertheless still in pre-trial detention, now under the charge of having participated in a group act of vandalism resulting in a broken window on a building belonging to the United Russia party.
Many disturbing signs of violation of his due legal process have been reported by the press and by human rights activists. These include torture, harassment of his relatives by local police, and a smear campaign involving homophobic slurs in the media. He has also been denied access to his scientific work. It is difficult to see how the charge of minor vandalism could warrant a year of pre-trial detention and this mistreatment. “Memorial”, the oldest Russian human rights organization, lists Azat Miftakhov as a political prisoner.
Please join many prominent mathematicians and sign a petition protesting Azat Miftakhov’s treatment here! The text above is not my own, but copied from the American Mathematical Society, who is also protesting this outrage. For more information go here.
December 19, 2020
Octonions and the Standard Model (Part 11)
Posted by John Baez
We can think of the exceptional Jordan algebra as a funny sort of spacetime. This spacetime is 27-dimensional, with light rays through the origin moving on a lightcone given by a cubic equation instead of the usual
in 4-dimensional Minkowski spacetime. But removing this lightcone still chops spacetime into 3 connected components: the past, the future, and the regions you can’t reach from the origin without exceeding the speed of light. The future is still a convex cone, and so is the past. So causality still makes sense like it does in special relativity.
At some point I got interested in seeing what physics would be like in this funny spacetime. Greg Egan and John Huerta joined me in figuring out the very basics of what quantum field theory would be like in this world. Namely, we figured out a bit about what kinds of particles are possible.
One difference is that we must replace the usual Lorentz group with the 78-dimensional group . But an even bigger difference is this. In 4d Minkowski space, every point in your field of view acts essentially like every other, if you turn your head. But in our 27-dimensional spacetime, the analogous fact fails! There is a ‘sky within the sky’: some particles moving at the speed of light can only be seen in certain directions. Thus, the classification of particles that move at the speed of light is much more baroque.
This is a big digression from my main quest here: explaining how people have tried to relate the octonions to the Standard Model. But it would be a shame not to make our results public, and now is a good time.
December 16, 2020
Octonions and the Standard Model (Part 10)
Posted by John Baez
The Dynkin diagram of has 2-fold symmetry:
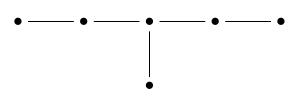
So, this Lie group has a nontrivial outer automorphism of order 2. This corresponds to duality in octonionic projective plane geometry! There’s an octonionic projective plane on which acts. But there’s also a dual octonionic projective plane . Points in the dual plane are lines in the original one, and vice versa. And these two projective planes are not isomorphic as spaces on which the group acts. Instead, there’s a bijection
such that acting by and then applying is the same as applying and then acting by , where is what you get when you apply the outer automorphism to .
Similarly, the group acts on the exceptional Jordan algebra and its dual, but these are not isomorphic as representations of . Instead they’re only isomorphic up to an outer automorphism.
Today I want to tell you about invariant structures on the exceptional Jordan algebra and its dual. But a lot of this stuff applies more generally.
December 13, 2020
The Lie of “It’s Just Math”
Posted by Tom Leinster
Jade Master at Riverside has written a short, important and lucid article about military funding of math, The Lie of “It’s Just Math”, accompanied by a call to action:
Fellow mathematicians, it’s time to stop letting the military benefit from our work.
Military involvement in math is particularly an issue in applied category theory, and particularly an issue in the USA. But the principles that Jade pithily expresses are universal:
The [US Department of Defense’s] real goal is not just the math you produce, they want to gain access to your mathematical community.
Your math is not too abstract to be useful.
The DoD wants to normalize themselves in your non-mathematical communities.
The DoD will lie to you.
Mathematicians are generally highly reluctant to talk about the human impact of what we do and the choices we make. For that reason, we’re not very practised at it. But Jade’s article deserves wide discussion, and I hope it gets it.
December 10, 2020
Bernoulli Numbers and the J-homomorphism
Posted by John Baez
I’m planning to stop teaching at U. C. Riverside in June 2021. I’ll only be 60, but what’s the use of quitting work when you’re too old to have fun?
I want to spend more time doing research and writing expository papers and books, and I’ve saved up enough money to do this. I’ll still do serious work, like trying to save the planet with applied category theory. But I’ll also delve into all sorts of puzzles that I haven’t had enough time for yet.
Here’s one. You may have heard about the funny way the number 24 shows up in the homotopy groups of spheres:
whenever is big enough, namely . If you try to figure out where this comes from, you’re led back to a map
called the quaternionic Hopf fibration. This by itself doesn’t make clear where the 24 is coming from — but you can’t help but notice that when you pack equal-sized balls as densely as is known to be possible in the quaternions, each one touches 24 others.
Coincidence? Maybe! But it’s also true that
when is big enough. And if you try to figure out where this comes from, you’re led back to a map
called the octonionic Hopf fibration. And you can’t help but notice that when you pack equal-sized balls as densely as possible in the octonions, each one touches 240 others!
December 9, 2020
The Algebraic K-Theory of the Integers
Posted by John Baez
The category of groups and isomorphisms between these is symmetric monoidal under . You can build a space out of simplexes where the 0-simplexes are objects of this category, the 1-simplexes are morphisms, the 2-simplexes are commutative triangles, the 3-simplexes are commutative tetrahedra, and so on forever. This space has an operation, coming from , that obeys the commutative monoid axioms up to homotopy. If you ‘group complete’ this space by throwing in formal inverses, you get a space that’s an abelian group up to homotopy. It’s called the algebraic -theory spectrum of the integers.
The algebraic -theory spectrum of the integers has homotopy groups , , , and so on. These groups are called the algebraic -theory groups of the integers, .
December 7, 2020
Applied Compositional Thinking for Engineers
Posted by John Baez
Hey! There’s a new online course coming up!
• Applied Compositional Thinking for Engineers. January 7, 8, 11-15, 20-22, and 25-29, 2021. Taught by Andrea Censi, Jonathan Lorand and Gioele Zardini.
It’s not an accident that the acronym for “Compositional Thinking” is “CT”.
December 6, 2020
Mathematical Phantoms
Posted by John Baez
A ‘mathematical phantom’ is a mathematical object that doesn’t exist in a literal sense, but nonetheless acts as if it did, casting a spell on surrounding areas of mathematics. The most famous example is the field with one element. Another is Deligne’s St, the symmetric group on elements, where is not a natural number. Yet another is G3, a phantom Lie group related to G2, the automorphism group of the octonions.
What’s your favorite mathematical phantom? My examples are all algebraic. Does only algebra have enough rigidity to create the patterns that summon up phantom objects? What about topology or combinatorics or analysis? Okay, G3 is really a creature from homotopy theory, but of a very algebraic sort.
Last night I met another phantom.
The Liquid Tensor Experiment
Posted by David Corfield
Peter Scholze has just published a challenge to the automated mathematical formalisation community in a post – Liquid tensor experiment – on Kevin Buzzard’s blog. Peter explains there the motivation for the theorem he would like to be formalised, and his reasons to want a formal computer-checked proof.
I see a couple of Café interests intertwined here: formalisation in dependent type theory, and the nature of (mathematical) space.
Regarding the former, there was an intense discussion recently on MathOverflow arising from a comment on the advantages of dependent type theory by Kevin, who for some time has been promoting the prover Lean as the best means to formalise the mathematics of typical mathematics departments.
In the comments to the main question, there is some discussion of why much more has been achieved in this regard by Lean compared with HoTT/Univalent Foundations approaches. We’ve heard plenty about this latter approach at the Café, in particular about its use to develop a kind of synthetic mathematics, due to HoTT being the internal language of -toposes. At the end of the references in the last link are some articles using modal HoTT, in particular relating to the cohesive modalities, as in Mike’s
Brouwer’s fixed-point theorem in real-cohesive homotopy type theory, Mathematical Structures in Computer Science Vol 28(6), (2018): pp. 856-941 (arXiv:1509.07584).
December 4, 2020
Entropy and Diversity: The Axiomatic Approach
Posted by Tom Leinster
As Emily was kind enough to point out earlier, my new book is out on the arXiv!
It’s arXived by agreement with the wonderful Cambridge University Press, who will publish it in April 2021. You can pre-order it now, as the ideal festive gift for any friend who enjoys deferred gratification.
Entropy and Diversity on the arXiv
Posted by Emily Riehl
There’s a new entry in today’s arXiv listings:
Entropy and Diversity: The Axiomatic Approach, a viii + 442 pages book to be published by Cambridge University Press in April 2021.
Congratulations Tom! This is really something.
And even more impressively, this is the second published book that Tom has made freely available on the arXiv! His wonderful Basic Category Theory is there as well.
 Posts with this logo use
Posts with this logo use 















