December 28, 2015
A Compositional Framework for Passive Linear Networks
Posted by John Baez

My main interest these days is ‘network theory’. This means slightly different things to different people, but for me it’s the application of category theory to complex systems made from interacting parts, which can often be drawn using diagrams that look like graphs with extra labels. My dream is to set up a new kind of mathematics, applicable to living systems from cells to ecosystems. But I’ve been starting with more humble networks, like electrical circuits.
Brendan Fong, at Oxford and U. Penn, has been really crucial in developing this approach to network theory. Here’s our first paper:
• John Baez and Brendan Fong, A compositional framework for passive linear networks.
While my paper with Jason Erbele studied signal flow diagrams, this one focuses on circuit diagrams. The two are different, but closely related.
Instead of trying to explain the connection, let me just talk about this paper with Brendan. There’s a lot in here, so I’ll only explain the main result. It’s all about ‘black boxing’: hiding the details of a circuit and only remembering its behavior as seen from outside. But it involves fun stuff about symplectic geometry, and cospans, and Dirichlet forms, and other things.
December 22, 2015
Operads and Phylogenetic Trees
Posted by John Baez
A few years ago, after hearing Susan Holmes speak about the mathematics of phylogenetic trees, I became interested in their connection to algebraic topology. I wrote an article about it:
- John Baez, Operads and the tree of life, Azimuth, 6 July 2011.
In trying to the make the ideas precise I recruited the help of Nina Otter, who was then a graduate student at ETH Zürich. She came to Riverside and we started to work together.
Now Nina Otter is a grad student at Oxford working on mathematical biology with Heather Harrington. I visited her last summer and we made more progress… but then she realized that our paper needed another big theorem, a result relating our topology on the space of phylogenetic trees to the topology described by Susan Holmes and her coauthors here:
- Louis J. Billera, Susan P. Holmes and Karen Vogtmann, Geometry of the space of phylogenetic trees, Advances in Applied Mathematics 27 (2001), 733–767.
It took another half year to finish things up. I could never have done this myself.
But now we’re done! Here’s our paper:
- John Baez and Nina Otter, Operads and phylogenetic trees.
Let me tell you the basic idea….
December 8, 2015
Research Fellowships at Macquarie University
Posted by Emily Riehl
A little bird tells me that Macquarie University is hiring (even more) category theorists!
Specifically, they are offering two-year research fellowship positions, details of which can be found here.
Macquarie University, which is in greater Sydney, is the home for Centre of Australian Category Theory. As I’m sure many -Café readers can attest, it’s a wonderful place to visit, to live, and to work. Applications are due in January.
December 5, 2015
Globular
Posted by John Baez
guest post by Jamie Vicary
When you’re trying to prove something in a monoidal category, or a higher category, string diagrams are a really useful technique, especially when you’re trying to get an intuition for what you’re doing. But when it comes to writing up your results, the problems start to mount. For a complex proof, it’s hard to be sure your result is correct — a slip of the pen could lead to a false proof, and an error that’s hard to find. And writing up your results can be a huge time-sink, requiring weeks or months using a graphics package, all just for some nice pictures that tell you little about the correctness of the proof, and become useless if you decide to change your approach. Computers should be able help with all these things, in the way that proof assistants like Coq and Agda are allowing us to work with traditional syntactic proofs in a more sophisticated way.
The purpose of this post is to introduce Globular, a new proof assistant for working with higher-categorical proofs using string diagrams. It’s available at http://globular.science, with documentation on the nab. It’s web-based, so everything happens right in your browser: build formal proofs, visualize and step through them; keep your proofs private, share them with collaborators, or make them publicly available.
Before we get into the technical details, here’s a screenshot of Globular in action:
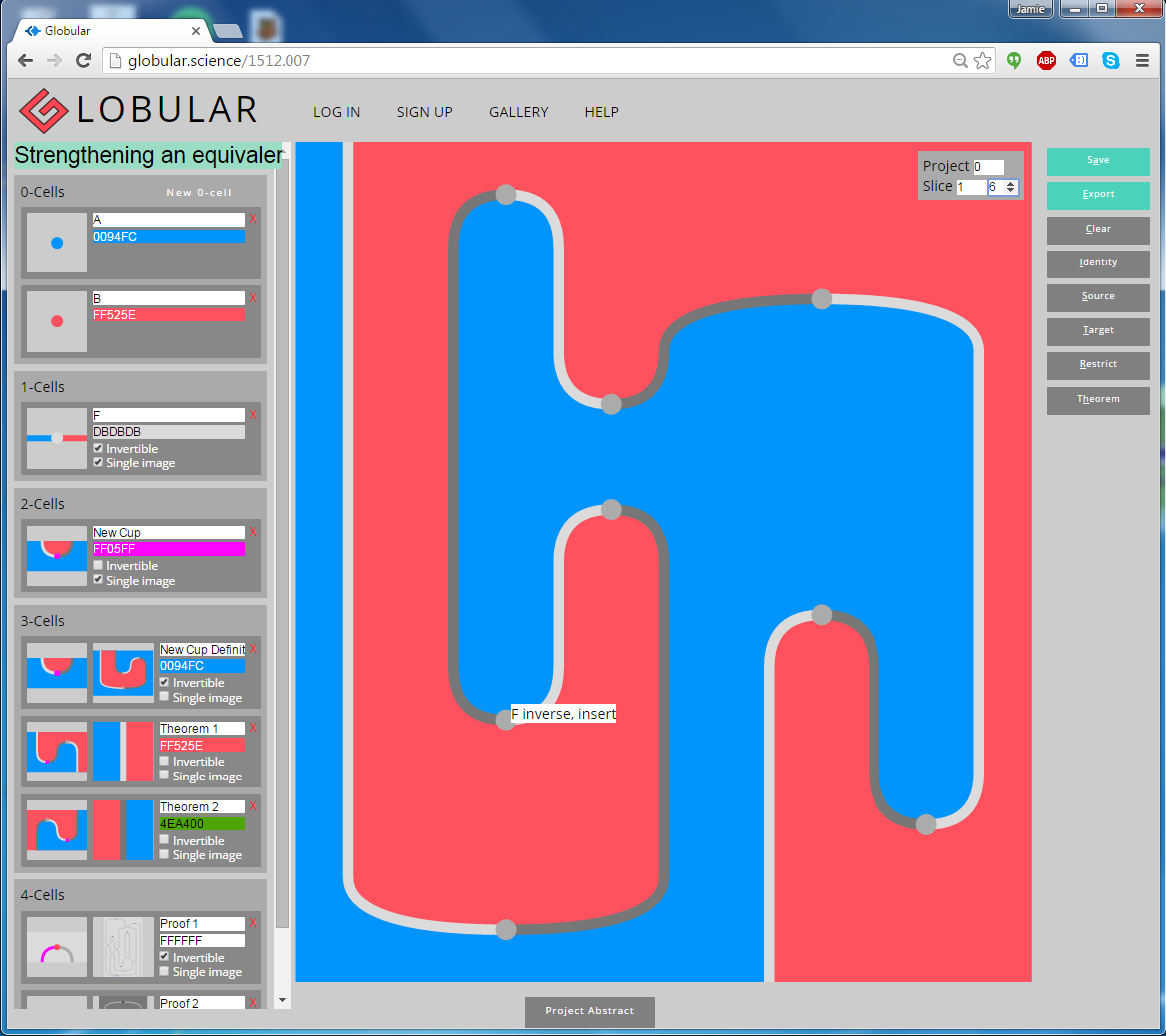
The main part of the screen shows a diagram, which in this case is 2-dimensional. It represents a composite 2-cell in a finitely-presented 2-category, with the blue and red regions representing objects, the lines representing 1-cells, and the vertices representing 2-cells. In fact, this 2d diagram is just an intermediate state of a 3d proof, through which we’re navigating with the ‘Slice’ controls in the top-right. The proof itself has been built up by composing the generators listed in the signature, down the left-hand side of the screen. (If you want to take a look at this proof yourself, you can go straight there; in the top-right, set ‘Project’ to 0, then increment the second ‘Slice’ counter to scroll through the proof.)
Globular has been developed so far in the Quantum Group in the Oxford Computer Science department, by Krzysztof Bar, Katherine Casey, Aleks Kissinger, Jamie Vicary and Caspar Wylie. We haven’t quite got around to it yet, but Globular will be open-source, and we’re really keen for people to get involved and help build the software — there’s a huge amount to do! If you want to help out, get in touch.
December 3, 2015
42
Posted by John Baez
In The Hitchhiker’s Guide to the Galaxy, the number 42 was revealed to be the Answer to the Ultimate Question of Life, the Universe, and Everything. But we never learned what the question was!
That’s what I’ll explain this Saturday in Montreal.
My talk is part of the Canadian Mathematical Society winter meeting. But it’s open to the public, and I’ll keep the math simple and fun. So, come along and bring your kids!
It’s from 6 to 7 pm on December 5th at the Hyatt Regency Montreal, at 1255 Jeanne-Mance. It’s in “Rooms Soprano A & B”, but I won’t be singing — they must have confused me with my cousin Joan.
 Posts with this logo use
Posts with this logo use 














