January 6, 2026
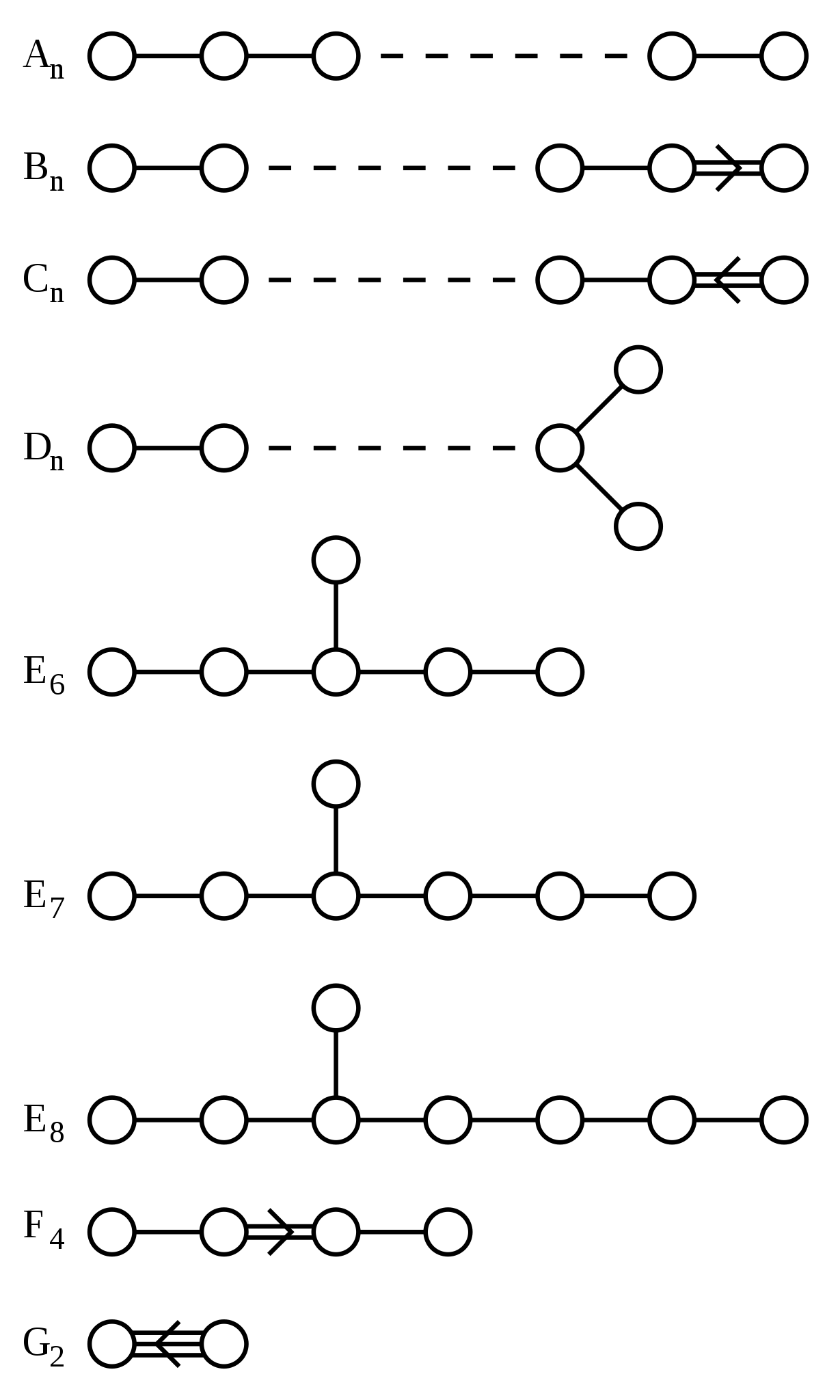
Coxeter and Dynkin Diagrams
Posted by John Baez
Dynkin diagrams have always fascinated me. They are magically potent language — you can do so much with them!
December 7, 2025
Octonions and the Standard Model (Part 13)
Posted by John Baez
When Lee and Yang suggested that the laws of physics might not be invariant under spatial reflection — that there’s a fundamental difference between left and right — Pauli was skeptical. In a letter to Victor Weisskopf in January 1957, he wrote:
“Ich glaube aber nicht, daß der Herrgott ein schwacher Linkshänder ist.”
(I do not believe that the Lord is a weak left-hander.)
But just two days after Pauli wrote this letter, Chien-Shiung Wu’s experiment confirmed that Lee and Yang were correct. There’s an inherent asymmetry in nature.
We can trace this back to how the ‘left-handed’ fermions and antifermions live in a different representation of the Standard Model gauge group than the right-handed ones. And when we try to build grand unified theories that take this into account, we run into the fact that while we can fit the Standard Model gauge group into in various ways, not all these ways produce the required asymmetry. There’s a way where it fits into , which is too symmetrical to work… and alas, this one has a nice octonionic description!
December 3, 2025
log|x| + C revisited
Posted by Mike Shulman
A while ago on this blog, Tom posted a question about teaching calculus: what do you tell students the value of is? The standard answer is , with an “arbitrary constant”. But that’s wrong if means (as we also usually tell students it does) the “most general antiderivative”, since
is a more general antiderivative, for two arbitrary constants and . (I’m writing for the natural logarithm function that Tom wrote as , for reasons that will become clear later.)
In the ensuing discussion it was mentioned that other standard indefinite integrals like are just as wrong. This happens whenever the domain of the integrand is disconnected: the “arbitrary constant” is really only locally constant. Moreover, Mark Meckes pointed out that believing in such formulas can lead to mistaken calculations such as
which is “clearly nonsense” since the integrand is everywhere positive.
In this post I want to argue that there’s actually a very natural perspective from which is correct, while is wrong for a different reason.
November 30, 2025
Octonions and the Standard Model (Part 12)
Posted by John Baez
Having spent a lot of time pondering the octonionic projective plane and its possible role in the Standard Model of particle physics, I’m now getting interested in the ‘bioctonionic plane’, which is based on the bioctonions rather than the octonions .
The bioctonionic plane also has intriguing mathematically connections to the Standard Model. But it’s not a projective plane in the axiomatic sense — and it can’t be constructed by straightforwardly copying the way you build a projective plane over a division algebra, since unlike the octonions, the bioctonions are not a division algebra. Nonetheless we can define points and lines in the bioctonionic plane. The twist is that now some pairs of distinct lines intersect in more than one point — and dually, some pairs of distinct points lie on more than one line. It obeys some subtler axioms, so people call it a Hjelmslev plane.
I am not ready to give a really good explanation of the bioctonionic plane! Instead, I just want to lay out some basic facts about how it fits into mathematics — and possibly physics.
November 22, 2025
Beyond the Geometry of Music
Posted by John Baez
Yesterday I had a great conversation with Dmitri Tymoczko about groupoids in music theory. But at this Higgs Centre Colloquium, he preferred to downplay groupoids and talk in a way physicists would enjoy more. Click here to watch his talk!
November 5, 2025
The Inverse Cube Force Law
Posted by John Baez
Here’s a draft of my next column for the Notices of the American Mathematical Society. It’s about the inverse cube force law in classical mechanics.
November 3, 2025
Second Quantization and the Kepler Problem
Posted by John Baez
The poet Blake wrote that you can see a world in a grain of sand. But even better, you can see a universe in an atom!
Bound states of hydrogen atom correspond to states of a massless quantum particle moving at the speed of light around the Einstein universe — a closed, static universe where space is a 3-sphere. We need to use a spin-½ particle to account for the spin of the electron. The states of the massless spin-½ particle where it forms a standing wave then correspond to the orbitals of the hydrogen atom. This explains the secret 4-dimensional rotation symmetry of the hydrogen atom.
In fact, you can develop this idea to the point of getting the periodic table of elements from a quantum field theory on the Einstein universe! I worked that out here:
but you can see a more gentle explanation in the following series of blog articles.
November 2, 2025
Dynamics in Jordan Algebras
Posted by John Baez
In ordinary quantum mechanics, in the special case where observables are described as self-adjoint complex matrices, we can describe time evolution of an observable using Heisenberg’s equation
where is a fixed self-adjoint matrix called the Hamiltonian. This framework is great when we want to focus on observables rather than states. But Heisenberg’s equation doesn’t make sense in a general Jordan algebra. In this stripped-down framework, all we can do is raise observables to powers and take real linear combinations of them. This lets us define a ‘Jordan product’ of observables:
but not commutators and not multiplication by . What do we do then?
October 27, 2025
Applied Category Theory 2026
Posted by John Baez
The next annual conference on applied category theory is in Estonia!
- Applied Category Theory 2026, Tallinn, Estonia, 6–10 July, 2026. Preceded by the Adjoint School Research Week, 29 June – 3 July.
For more details, read on!
October 6, 2025
A Complex Qutrit Inside an Octonionic One
Posted by John Baez
Dubois-Violette and Todorov noticed that the Standard Model gauge group is the intersection of two maximal subgroups of . I’m trying to understand these subgroups better.
September 13, 2025
A Shadow of Triality?
Posted by John Baez
It’s well known that you can construct the octonions using triality. One statement of triality is that has nontrivial outer automorphisms of order 3. On the other hand, the octonions have nontrivial inner automorphisms of order 3. My question: can we deduce one of these facts from the other?
August 29, 2025
Equivalence via Surjections
Posted by Tom Leinster
Pick a type of categorical structure: say bicategories, or monoidal categories, or whatever you like. Some of the functors between structures are equivalences, in whatever the appropriate sense might be. And some of those equivalences have one or both of these two properties:
They’re not just essentially surjective in every dimension — they’re actually surjective in every dimension.
They don’t just preserve the structure up to isomorphism or equivalence — they strictly preserve it.
Call an equivalence with both these properties a strict surjective equivalence. So a strict surjective equivalence is an equivalence of a very special and easy kind.
General principle: the standard notion of equivalence between structures is generated by just these very special ones. For example, two bicategories are biequivalent if and only if they can be linked up by a zigzag of strict surjective equivalences.
Why should we care? Because there are some types of structure where the right notion of equivalence isn’t clear, and this principle guides us to it. For example, it tells us the right notion of equivalence for double categories.
All this is done in my new paper:
Tom Leinster, Equivalence via surjections. arXiv:2508.20555, 2025.
August 28, 2025
Burrito Monads, Arrow Kitchens, and Freyd Category Recipes
Posted by Tom Leinster
Guest post by Khyathi Komalan and Andrew Krenz
From Lawvere’s Hegelian taco to Baez’s layer cake analogy to Eugenia Cheng’s How to Bake Pi, categorists have cultivated a rich tradition of culinary metaphors and similes. A well-known example in the world of computation is Mark Dominus’s “monads are like burritos” — where a tortilla (computational context) wraps diverse ingredients (values) to create a cohesive entity (effectful value) whose burrito structure is maintained as the meal moves down the assembly line (undergoes computations).
August 14, 2025
Safeguarded AI Meeting
Posted by John Baez
This week, 50 category theorists and software engineers working on “safeguarded AI” are meeting in Bristol. They’re being funded by £59 million from ARIA, the UK’s Advanced Research and Invention Agency.
The basic idea is to develop a mathematical box that can contain a powerful genie. More precisely:
By combining scientific world models and mathematical proofs we will aim to construct a ‘gatekeeper’, an AI system tasked with understanding and reducing the risks of other AI agents. In doing so we’ll develop quantitative safety guarantees for AI in the way we have come to expect for nuclear power and passenger aviation.
August 5, 2025
(BT) Diversity from (LC) Diversity
Posted by Tom Leinster
Guest post by Mark Meckes
Around 2010, in papers that both appeared in print in 2012, two different mathematical notions were introduced and given the name “diversity”.
One, introduced by Tom Leinster and Christina Cobbold, is already familiar to regular readers of this blog. Say is a finite set, and for each we have a number that specifies how “similar” and are. (Typically we also assume .) Fix a parameter . If is a probability distribution on , then the quantity (with the cases defined by taking limits) can be interpreted as the “effective number of points” in , taking into account both the similarities between points as quantified by and the weights specified by . Its logarithm is a refinement of the -Rényi entropy of . The main motivating example is when is a set of species of organisms present in an ecosystem, and quantifies the “effective number of species” in , accounting for both similarities between species and their relative abundances. This family of quantities turns out to subsume many of the diversity measures previously introduced in the theoretical ecology literature, and they are now often referred to as Leinster–Cobbold diversities.
 Posts with this logo use
Posts with this logo use 














